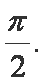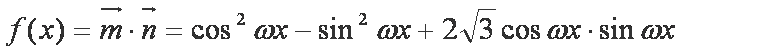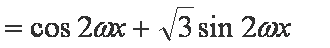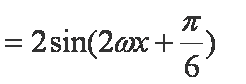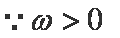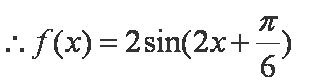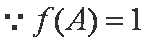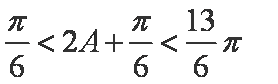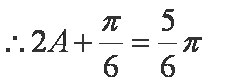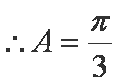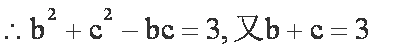- 三角恒等变换
- 共864题
已知函数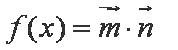
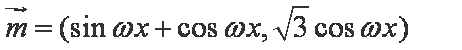
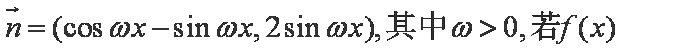
(1)求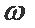
(2)在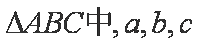
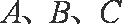
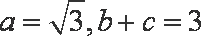
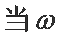
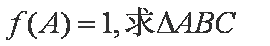
正确答案
见解析
解析
解析:(1)
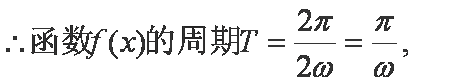
解得
(2)由(1)可知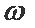

由余弦定理知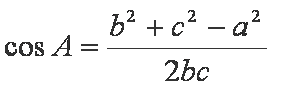
联立解得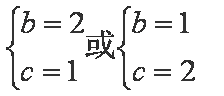
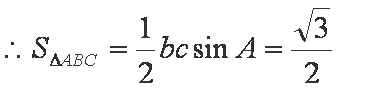
知识点
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC, AB⊥BC,AB=AD=1,BC=2,又PB⊥平面ABCD,且PB=1,点E在棱PD上,且DE=2PE.
(1)求证:BE⊥平面PCD;
(2)求二面角A一PD-B的大小.
正确答案
解析
如图,以B为原点,分别以BC、BA、BP为x、y、z轴,建立空间直角坐标系,则B(0,0,0),C(2,0,0),A(0,1,0),D(1,1,0),P(0,0,1),又DE=2PE,
∴E(,,).(2分)
(1)∵=(,,),=(1,1,-1),=(2,0,-1),
∴·=×1+×1+×(-1)=0,
·=×2+×0+×(-1)=0.
∴BE⊥PD,BE⊥PC,又PD∩PC=P,
∴BE⊥平面PCD.(8分)
(2)设平面PAD的一个法向量为n0=(x,y,z),
则由得
令z=1,则n0=(0,1,1)。
又=(0,0,1),设平面PBD的法向量为n1=(x1,y1,z1),
则由得
令x1=1,则n1=(1,-1,0),
∴cos〈n0,n1〉===-,
∴〈n0,n1〉=120°.
又二面角A—PD—B为锐二面角,故二面角A—PD—B的大小为60°.(13分)
知识点
已知函数
(1)求函数
(2)若存在


(3)对任意的


正确答案
见解析
解析
(1)

函数

(2)当

(理)存在


(3)存在唯一的

(文理)当


设

得
所以
∵
∴



知识点
如图,长方体






(1)求证:

(2)求证:平面

(3)求二面角
正确答案
见解析。
解析
(1)连接






又




(2)计算可得


又




又


(3)由(2)知














知识点
已知函数
(1)求函数

(2)求函数
正确答案
见解析。
解析
(1)
令 
函数


(2) 由
得: 
故
知识点
将函数f(x)=


正确答案
解析
将f(x)=sin 2x-cos 2x=2sin(2x-)的图象向左平移m个单位,得函数g(x)=2sin(2x+2m-)的图象,则由题意得2×+2m-=kπ+(k∈Z),即有m=+(k∈Z),∵m>-,∴当k=-1时,mmin=-.
知识点
已知函数


正确答案
解析
由函数



知识点
已知向量




(1)求
(2)当


正确答案
见解析。
解析
(1) 




∵θ∈[π,2π],∴



(2) 由已知

又

∵θ∈[π,2π]∴
知识点
如图,在圆







(1)当点



(2)若圆





正确答案
见解析
解析
本小题考查椭圆的标准方程与性质、直线与圆锥曲线的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想等。
(1)设





即点


(2)解法一:
(i) 当直线




(ii)当直线


因为直线



又直线



所以直线


由




综上(i)(ii)知,直线

解法二 :设


(i)当





(ii)当



令



所以直线


由





综上(i)(ii)知,直线

知识点
已知函数




(1)求函数
(2)把函数


正确答案
见解析
解析
解:(1)


依题意:











(2)把函数



平移后的图象对应的函数解析式为:
知识点
扫码查看完整答案与解析