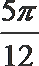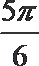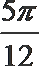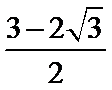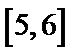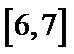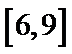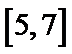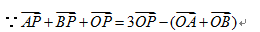- 三角恒等变换
- 共864题
6.要得到y=sin2x-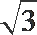
正确答案
解析
本题属于三角函数中的基本问题,题目的难度是逐渐由易到难。注意化简时对φ的选取。
考查方向
本题主要考查了三角函数的图象与性质,在近几年的各省高考题出现的频率非常高,常与三角恒等变形公式,函数单调性、周期性、对称型、奇偶性等知识点交汇命题。
解题思路
无
易错点
本题易在公式化简上发生错误。
知识点
17.



(Ⅰ)求角
(Ⅱ)若

正确答案
(Ⅰ)
(Ⅱ)
解析
试题分析:本题属于解三角形中的基本问题,难度不大。此类问题主要应用正(余)弦定理进行恒等变换;注意边和角的统一。
(Ⅰ)在

所以
因为
所以

解得
因为

(Ⅱ)由正弦定理,
所以

因为

所以


考查方向
解题思路
本题主要考查正(余)弦定理、和(差)角公式和三角函数的恒等变换等知识,
解题步骤如下:
利用降幂公式和三角变换化成关于cosC的一元二次方程;
利用正弦定理把边化成角,从而求出
易错点
第一问中降幂公式往往会出错;
第二问中角A的范围和
知识点
4.函数
正确答案
解析





考查方向
解题思路
1.先将
2.利用对称中心的坐标公式求出对称中心。
易错点
1.误认为对称中心的纵坐标为0,导致误选B;
2.不将
知识点
15.函数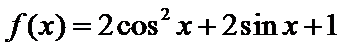
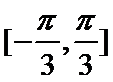
正确答案
解析
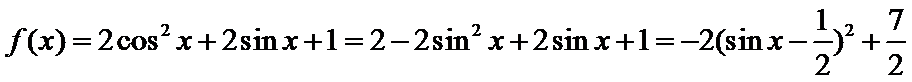
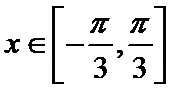
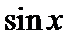
考查方向
解题思路
本题属于简单题,
(1)利用同角三角函数的关系化成同一三角函数并配方
(2)利用二次函数的图像求最值
易错点
利用二次函数的图像求最值
知识点
9.在平面直角坐标系
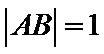
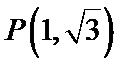
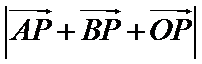
正确答案
解析
考查方向
解题思路
使用向量的几何意义,
易错点
本题易错于几何意义的转换,或者在使用坐标化的过程中A,B两点的形成过程,代数法构建过程繁琐,学生易计算出错,
知识点
17.
(1)求
(2)若


正确答案
(1)
(2)
解析
本题属于三角恒等变形和解三角形的基本问题
(1)直接按照步骤来求
(2)要注意观察,然后合理地选择公式来解题。
(1) 




(2)



考查方向
本题考查了三角函数的基本公式即:诱导公式、同角关系式、两角和差公式和二倍角公式在化简中的应用,内角和定理、正余弦定理在解三角形的应用;
易错点
1、对
2、根据条件合理选择定理来解三角形。
知识点
已知





正确答案
解析
由







考查方向
本题主要考查了矩阵的概念,三角函数图像与性质的综合应用
易错点
函数平移的对象是x,这是解决函数平移的问题的关键
知识点
已知角







正确答案
解:(1)由

且

∴

∴
(2)由余弦定理得
,而∵
由


当且仅当
又


所以

解析
本题属于三角函数的基本问题,题目的难度是中等,本题的关键是:
(1)、向量的基本运算以及三角函数恒等变换的应用;
(2)、余弦定理与基本不等式之间的应用,一直是考试的热点问题,
考查方向
本题考查了向量运算、三角函数恒等变换、正弦定理和余弦定理的综合应用
易错点
向量的运算、余弦定理的应用,需要注意
知识点
6.为了得到函数
正确答案
解析
函数y=


∵sin(4x﹣

∴为了得到函数y=


故选:A.
考查方向
解题思路
1、先根据题意化原函数为

易错点
1、本题在化简成“
知识点
15.已知函数
(Ⅰ)求函数
(Ⅱ)求函数

正确答案
(Ⅰ)
(Ⅱ)0
解析
(Ⅰ)因为



(Ⅱ)因为


当


当


因为
所以函数

考查方向
本题主要考察了三角函数的图象与性质,属于中档题,是高考的热点,解决此类题的关键:一是会化简,熟悉三角恒等变形公式;二是会用性质,熟悉单调性、周期性、对称性、和最值问题。
易错点
1、本题易在化简的过程汇总发生错误,导致最小正周期算错 。
2、单调性分析不全面,导致题目无法进行。
知识点
扫码查看完整答案与解析