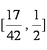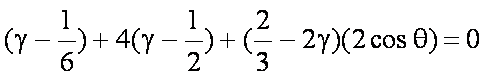- 三角恒等变换
- 共864题
在锐角



正确答案
解析
略
知识点
已知函数
(1)试判断函数
(2)若

(3)求证: 
正确答案
见解析。
解析
(1)





(2)

再令








(3)方法1: 由(2)知:
令




叠加得:

方法2:用数学归纳法证明(略)。
知识点
圆心为(1,1)且与直线x+y=4相切的圆的方程是 。
正确答案
(x﹣1)2+(y﹣1)2=2
解析
圆心到直线的距离就是圆的半径:r=

所以圆的标准方程:(x﹣1)2+(y﹣1)2=2
故答案为:(x﹣1)2+(y﹣1)2=2
知识点
已知函数

(1) 求f(x)的解析式;
(2)在△ABC中,AC=2,BC=3,A为锐角,且
正确答案
见解析。
解析
(1)
(2)


知识点
在







正确答案
见解析。
解析
。在


所以
又

因为



所以,

由①、②可知 
所以
知识点
在△OAB的边OA、OB上分别有一点P、Q,已知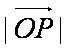
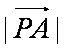
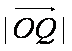
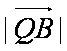
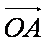
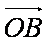
(1)用a与 b表示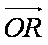
(2)过R作RH⊥AB,垂足为H,若| a|=1, | b|=2, a与 b的夹角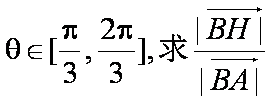
正确答案
(1)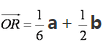
解析
解析:(1)由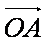
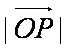
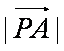
可得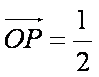
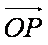
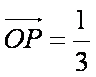
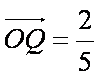
设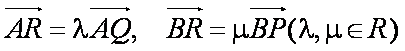
则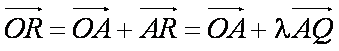
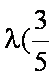
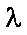
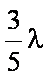
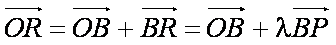
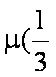
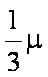
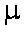
∵向量a与b不共线, ∴
∴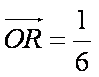

(2)设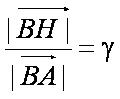
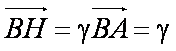
∴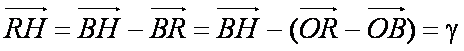


=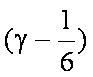
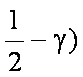
∵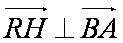
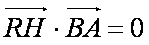
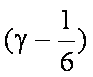
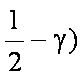
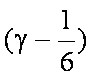
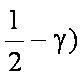
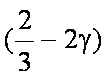
又∵|a|=1, |b|=2, a·b=|a||b|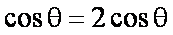
∴
∴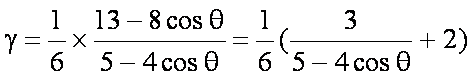
∵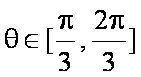
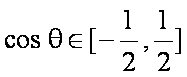

∴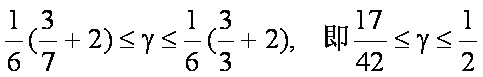
故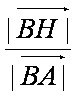
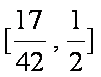
知识点
在等腰梯形












正确答案
解析
如图,过













故
知识点
在△ABC中,角A、B、C的所对应边分别为a,b,c,且
(1)求c的值;
(2)求
正确答案
见解析
解析
解:(1)根据正弦定理,
(2)根据余弦定理,得
于是
所以
知识点
在△ABC中,角A,B,C的对边分别为a,b,c。
(1)若cos(A+
(2)若cosA=
正确答案
见解析
解析
(1)在△ABC中,若cos(A+


化简可得



(2)若cosA=

由于sinA=



知识点
设数列




(1)若


(2)求
正确答案
见解析
解析
(1)在



由
相减可得


可见,

(2)由


即当

① 若



故
② 若
③ 若



于是当








知识点
扫码查看完整答案与解析