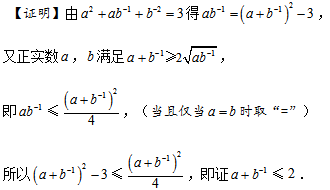- 三角恒等变换
- 共864题
14.在锐角三角形


正确答案
8;
解析
由

可得
由三角形

在(*)式两侧同时除以

又
则
由

令


由(#)得






当且仅当


解得


考查方向
解题思路
根据诱导公式、和差角公式化简,利用两边同除得到正切关系,应用正切公式的变形分析表示出
易错点
公式变形,函数关系转化,函数思想应用。
知识点
如图,
















20. 求

21. 已知警员的对讲机的有效通话距离是





正确答案
(1)

解析
试题分析: (1)由题意可得

(1)
记乙到


在

所以
考查方向
解题思路
解三角形时,有时可用正弦定理,有时也可用余弦定理,应注意用哪一个定理更方便、简捷.如果式子中含有角的余弦或边的二次式,要考虑用余弦定理;如果遇到的式子中含有角的正弦或边的一次式时,则考虑用正弦定理;以上特征都不明显时,则要考虑两个定理都有可能用到.
易错点
实际问题数学模型的转化
正确答案
(2)

解析
试题分析:(2) 分段求出对应函数解析式,根据函数单调性求得最值即可.
(2)甲到达






当

当

所以
因为








考查方向
解题思路
分段求出各个段上的函数解析式及定义域.
易错点
分段函数单调性最值的求解
5.若
正确答案
知识点
在

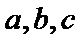
16.证明:
17.若

正确答案
由正弦定理得
故
于是
又




因此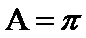

所以,
解析
见答案
考查方向
解题思路
先利用三角形正弦定理进行边角互化,再将角C用A,B表示,化简即可以得到结论
易错点
两正弦相等可能会缺少两角互补的情况
正确答案

解析
由
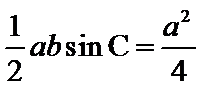

因




当



综上,

考查方向
解题思路
选择恰当的面积公式,进行边角互化。
易错点
两正弦相等可能会缺少两角互补的情况
3.在△ABC中,若

正确答案
解析
设
由余弦定理得:



考查方向
解题思路
利用正、余弦定理解三角形其关键是运用两个定理实现边角互化,从而达到知三求三的目的.本题直接根据余弦定理进行计算即可。
易错点
对余弦定理不熟悉导致出错。
知识点
13.已知三棱镜的四个面都是腰长为2的等腰三角形,该三棱锥的正视图如图所示,则该三棱锥的体积是 。
正确答案
解析
由题可知,∵三棱锥每个面都是腰为2的等腰三角形,由正视图可得如下俯视图,且三棱锥高为
考查方向
解题思路
本题考查三视图,考查几何体体积,考查学生的识图能力.解题时要求我们根据三视图想象出几何体的形状,由三视图得出几何体的尺寸,为此我们必须掌握基本几何体(柱、锥、台、球)的三视图以及各种组合体的三视图.
易错点
本题考查三视图,考查几何体体积,考查学生的识图能力.在识图时易错。
知识点
12.在




正确答案
1
解析

考查方向
解题思路
题目所求分式的分子为二倍角正弦,应用二倍角的正弦公式进行恒等变形,变形后为角的正弦、余弦式,灵活运用正弦定理和余弦定理进行角化边,再把边长代入求值.
易错点
灵活使用正弦定理、余弦定理进行边化角、角化边.
知识点
如图,长方体ABCD-A1B1C1D1中AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F。过带你E,F的平面α与此长方体的面相交,交线围成一个正方形
21.在图中画出这个正方形(不必说出画法和理由)
22.求直线AF与平面α所成角的正弦值
正确答案
正确答案
21.【选做题】
在A、B、C、D四小题中只能选做两小题。解答时应写出文字说明、证明过程或演算步骤。
A.几何证明选讲
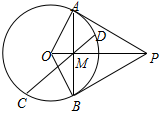
如图,从圆O外一点P作圆O的两条切线,切点分别为A,B,AB与OP交于点M,设CD为过点M且不过圆O的一条弦,求证:O、C、P、D四点共圆。
B.矩阵与变换
设矩阵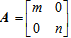
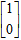
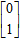
C.极坐标与参数方程
在极坐标系中,已知点O(0,0),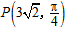
D.不等式选讲
设正实数a,b满足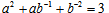
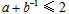
正确答案
A.
B.
C.
D.
解析
解析已在路上飞奔,马上就到!
知识点
6.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析