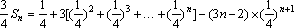- 三角恒等变换
- 共864题
一个几何体的三视图如图所示,其中主视图和左视图 是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积为 ( )
正确答案
解析
略。
知识点
函数
正确答案
解析
略
知识点
某校同学设计一个如图所示的“蝴蝶形图案(阴影区域)”,其中









求抛物线
如果使“蝴蝶形图案”的面积最小,求
正确答案
(1)
解析
(1) 由抛物线


(2) 设
所以,
解得
同理:
“蝴蝶形图案”的面积
令
则


知识点
如图,











正确答案
2
解析










知识点
已知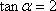
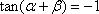
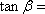
正确答案
3
解析
略
知识点
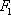
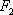

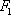
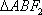
正确答案
解析
略
知识点
在


正确答案
2
解析

知识点
在数列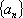
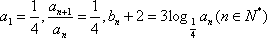
(1)求数列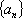
(2)求证:数列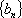
(3)设数列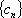

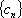
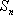
正确答案
见解析。
解析
(1)∵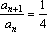
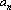


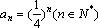
(2)∵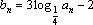
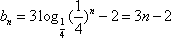
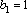
公差d=3,∴数列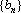
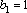
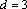
(3)由(1)、(2)知,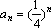

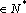
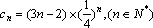
∴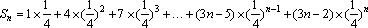
于是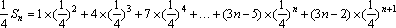
两式①-②相减得
=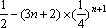
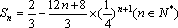
知识点
已知二次函数



(1)求a的值;
(2)

(3)若m=1,且x>0,求证:
正确答案
见解析。
解析
(1)解:∵关于


即不等式

∴
∴
∴
∴
(2)解法1:由(1)得
∴

∴
方程

①当

则



∴函数


∴函数

②当



若
故

∴函数

∴函数
若
则





∴函数



∴函数


综上所述, 当



当




(其中

解法2:由(1)得
∴

∴
若函数


令
得
则
方程(*)的两个实根为

设
①若



则



∴函数


∴函数

②若

又由(**)解得

故
则





∴函数



∴函数


综上所述, 当



当




(其中

(2)证法1:∵

∴

令
则

∵
∴

∴

证法2:下面用数学归纳法证明不等式
① 当


② 假设当


则

也就是说,当
由①②可得,对


知识点
已知锐角△ABC的面积等于
(1)求
(2)求
正确答案
见解析。
解析
(1)∵
∴
又△ABC是锐角三角形,∴
∴
(2)由余弦定理
∴
由正弦定理得
又B为锐角,得
∴
知识点
扫码查看完整答案与解析