- 集合的含义
- 共531题
设不等式

(1)求集合
(2)若




正确答案
(1)
(2)
解析
(1)由
所以
(2)由(1)和
所以
故
知识点
下列函数中,满足“
正确答案
解析
知识点
复数
正确答案
解析
分母实数化,可求得
知识点
给定常数



(1)若



(3)是否存在


正确答案
见解析。
解析
(1)因为


(2)要证明原命题,只需证明

即只需证明
若

若

综上,

(3)由(2)知,若

此时,
即
故
即
当



若

此时,
综上,满足题意的

知识点






正确答案
解析
由于,(z﹣

又z+
由①②解得z=1﹣i
知识点
在直接坐标系





(1)已知在极坐标(与直角坐标系






(2)设点


正确答案
(1)点P在直线
(2)
解析
(1)把极坐标系下的点
因为点P的直角坐标(0,4)满足直线

所以点P在直线
(2)因为点Q在曲线C上,故可设点Q的坐标为
从而点Q到直线

由此得,当
知识点
已知点E、F分别在正方体



正确答案
解析
延长EF交BC的延长线于P,则AP为面AEF与面ABC的交线,因为

知识点
已知函数f(x)是定义在R上的奇函数,当x≥0时,

正确答案
解析
当x≥0时,
f(x)=
由f(x)=x﹣3a2,x>2a2,得f(x)>﹣a2;
当a2<x<2a2时,f(x)=﹣a2;
由f(x)=﹣x,0≤x≤a2,得f(x)≥﹣a2。
∴当x>0时,
∵函数f(x)为奇函数,
∴当x<0时,
∵对∀x∈R,都有f(x﹣1)≤f(x),
∴2a2﹣(﹣4a2)≤1,解得:
故实数a的取值范围是
知识点
已知等差数列
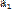

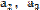
(1) 求数列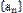
(2)记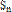
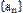
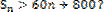
正确答案
见解析。
解析
(1)设数列{an}的公差为d,依题意,2,2+d,2+4d成比数列,故有(2+d)2=2(2+4d),
化简得d2﹣4d=0,解得d=0或4,
当d=0时,an=2,
当d=4时,an=2+(n﹣1)•4=4n﹣2。
(2)当an=2时,Sn=2n,显然2n<60n+800,
此时不存在正整数n,使得Sn>60n+800成立,
当an=4n﹣2时,Sn=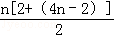
令2n2>60n+800,即n2﹣30n﹣400>0,
解得n>40,或n<﹣10(舍去),
此时存在正整数n,使得Sn>60n+800成立,n的最小值为41,
综上,当an=2时,不存在满足题意的正整数n,
当an=4n﹣2时,存在满足题意的正整数n,最小值为41
知识点
如图,正方形ABCD和正方形DEFG的边长分别为a,b(a<b),原点O为AD的中点,抛物线y2=2px(p>0)经过C,F两点,则
正确答案
解析
由题意,知

又C,F在抛物线y2=2px(p>0)上,
所以
由②÷①,得
解得
故
知识点
扫码查看完整答案与解析




































