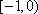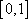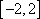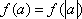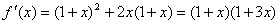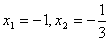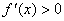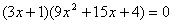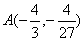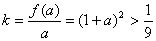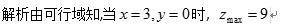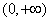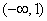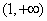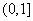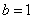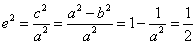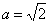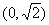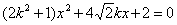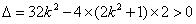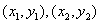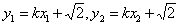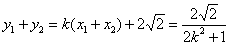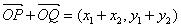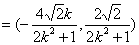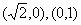- 分式不等式的解法
- 共109题
已知函数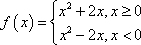
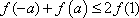

正确答案
解析
由偶函数定义可得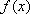
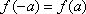

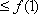
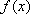




知识点
已知变量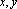
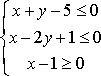

正确答案
9
解析
略
知识点
已知函数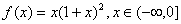
(1)求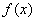
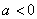
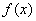
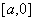

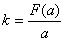
正确答案
见解析。
解析
(1)
由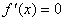
当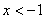
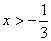
当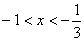
所以,有两个极值点: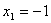
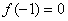
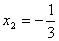
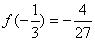
(2) 过点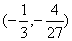
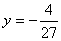
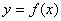
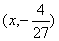
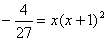
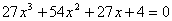
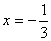
解得
当
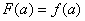
当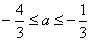
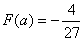


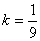
当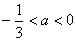
所以,对任意的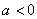
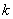
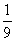
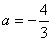
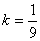
知识点
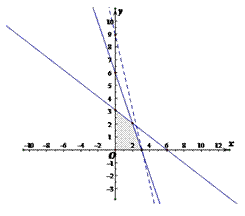
设实数x、y满足
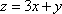
正确答案
9
解析
知识点
已知函数



正确答案
-1;
解析
略
知识点
若实数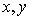
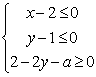
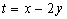
正确答案
解析
略
知识点
已知函数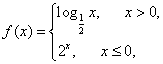
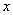


正确答案
解析
略
知识点
已知函数f(x)=
正确答案
解析
略
知识点
已知变量


正确答案
解析
略
知识点
在直角坐标系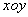
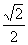
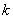
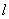
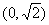
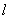
(1)求椭圆C的标准方程;
(2)求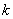
(3)若椭圆C的右端点和上端点分别为A、B,是否存在常数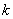
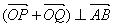
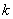
正确答案
见解析。
解析
(1)因为椭圆C以原点为中心,焦点在x轴上,
可设椭圆C的标准方程为: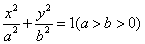
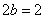
又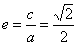
所以
所以椭圆C的标准方程为: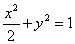
(2)因为斜率为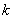
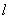
所以直线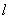
因为直线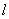
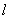
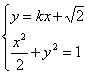
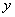
判别式
解得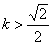
(3)设P、Q坐标分别为
则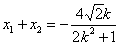
所以
所以
又椭圆C的右端点和上端点分别为A、B坐标为
所以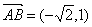
假设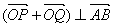
解得
故存在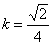
知识点
扫码查看完整答案与解析