- 命题的否定
- 共34题
1
题型:
单选题
|
设{an}是首项为正数的等比数列,公比为q,则“q<0”是“对任意的正整数n,a2n−1+a2n<0”的
正确答案
C
知识点
命题的否定
1
题型:
单选题
|
15.设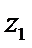
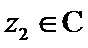
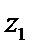
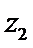
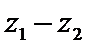
正确答案
B
解析
若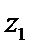
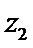
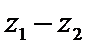
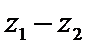
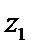
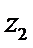
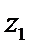
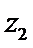
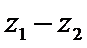
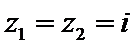
考查方向
本题主要考查充分条件和必要条件的判断,根据复数的有关概念进行判断是解决本题的关键.
解题思路
形如a+bi(a,b∈R)的数叫复数,其中a,b分别是它的实部和虚部.若b=0,则a+bi为实数;若b≠0,则a+bi为虚数;若a=0且b≠0,则a+bi为纯虚数.判断概念必须从其定义出发,不可想当然.
易错点
复数相等的条件
知识点
并集及其运算命题的否定
1
题型:
单选题
|
4. 下列叙述中正确的是( )
正确答案
D
解析
A.不正确,a<0不成立;B.不正确,如b=0; C不正确,命题“对任意



考查方向
本题考查主要命题及简易逻辑
解题思路
按照题中涉及到相关知识点,运用命题的知识点逐一排查。
易错点
不理解条件与结论之间的关系导致出错。全称命题的否定不理解。
知识点
充要条件的判定命题的否定
1
题型:
单选题
|
3.命题“

正确答案
D
解析
由于全称命题的否定为特称命题,
故“



故选D.
考查方向
本题主要考查了含有量词命题的否定形式.属于基础题.
解题思路
根据全称命题的否定是特称命题进行转化格式即可.
易错点
否定形式为:改量词,否结论.
知识点
命题的否定
1
题型:
单选题
|
2.命题“
正确答案
A
解析
因为特称命题的否定是全称命题,所以,命题“∃a∈[0,+∞),sina>a”的否定形式是∀a∈[0,+∞),sina≤a,故选:A.
考查方向
命题的否定
解题思路
利用特称命题的否定是全称命题写出结果即可
易错点
逻辑思维混乱
知识点
命题的否定
下一知识点 : 命题的真假判断与应用
扫码查看完整答案与解析