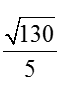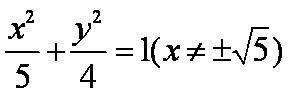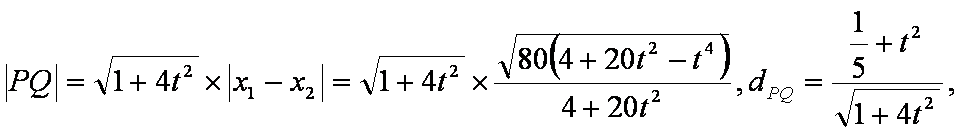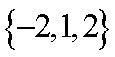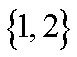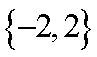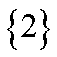- 相交弦所在直线的方程
- 共35题
1
题型:简答题
|
设平面内两定点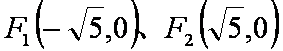
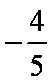
(1)求动点P的轨迹C1的方程;
(2)设M(0,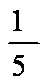
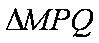
正确答案
(1)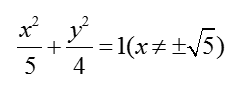
解析
解析:(1)设点P(x,y),依题意则有
……………4分
(2)设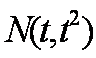
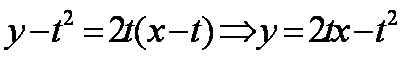
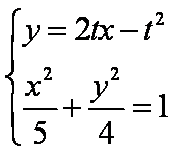
消去y整理得:,有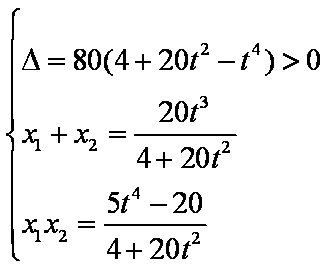
……………8分
而
………11分
由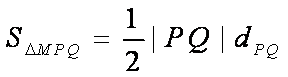
即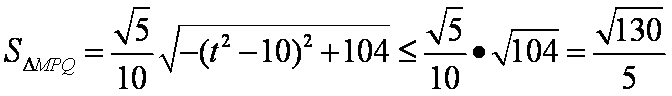
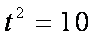
…………………13分
知识点
相交弦所在直线的方程
1
题型:
单选题
|
已知集合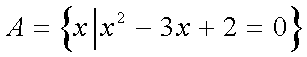
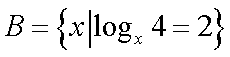
正确答案
B
解析
第一步开始识别条件:按照读题过程,先看到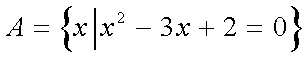
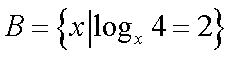
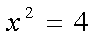
第二步转化条件:两个条件,顺手就转化到A={1,2},B={2}转化一念间
第三步看问来定向:看看题目的问题是啥,求的是并集。这就是方向。
第四步结论已出现:结论已经显然了,{1,2}。
知识点
相交弦所在直线的方程
1
题型:填空题
|
13.某学生在参加政、史、地三门课程的学业水平考试中,取得 







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
相交弦所在直线的方程
1
题型:简答题
|
16.已知函数
(1)求
(2)将



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
相交弦所在直线的方程
1
题型:填空题
|
13.今有直线







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
相交弦所在直线的方程
下一知识点 : 直线和圆的方程的应用
扫码查看完整答案与解析