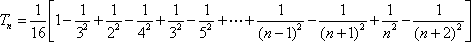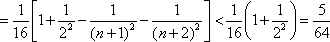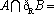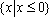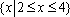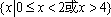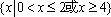· 直线与圆、圆与圆的位置关系

· 直线和圆的方程的应用

直线和圆的方程的应用
共43题

· 直线与圆、圆与圆的位置关系

· 直线和圆的方程的应用

直线和圆的方程的应用
共43题

热门试卷

X 查看更多试卷

1

题型：填空题

|

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

1

题型：简答题

|

简答题 · 12 分

正项数列{an}的前n项和Sn满足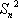：－（n2＋n－1）Sn－（n2＋n）＝0.

（1）求数列{an}的通项公式an；

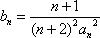
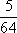
（2）令，数列{bn}的前n项和为Tn.证明：对于任意的n∈N*，都有Tn＜.

正确答案

见解析

解析

（1）解：由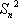－（n2＋n－1）Sn－（n2＋n）＝0，得[Sn－（n2＋n）]（Sn＋1）＝0.

由于{an}是正项数列，所以Sn>0，Sn＝n2＋n.

于是a1＝S1＝2，n≥2时，an＝Sn－Sn－1＝n2＋n－（n－1）2－（n－1）＝2n.

综上，数列{an}的通项an＝2n.

（2）证明：由于an＝2n，，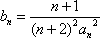

则.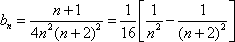

知识点

直线和圆的方程的应用

1

题型：单选题

|

单选题 · 5 分

已知全集为，集合，，则

A

B

C

D

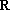
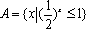
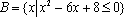
正确答案

C

解析

略

知识点

直线和圆的方程的应用

1

题型：单选题

|

单选题 · 5 分

设{an}是有正数组成的等比数列，为其前n项和。已知a2a4=1, ,则

A

B

C

D

正确答案

B

解析

由a2a4=1可得，因此，又因为，联力两式有，所以q=,所以，故选B。

知识点

直线和圆的方程的应用

1

题型：简答题

|

简答题 · 12 分

设函数.

（1）求的单调区间、最大值；

（2）讨论关于的方程根的个数。

正确答案

见解析。

解析

（1），

令，解得，令，解得

所以的单调递增区间为，单调递减区间为，

的最大值为

（2）令，

①当时

，所以

在时，函数的值域为，函数的值域为，所以在上，恒有，即，所以对任意大于零恒成立，所以在上单调递增；

②当时，

，所以，显然在时有函数恒成立，所以函数在时恒成立，所以对任意恒成立，所以在上单调递减；

由①②得，函数在上单调递增，在上单调递减，所以的最大值为

当，即时，方程有且只有一个根；

当，即时，方程有两个不等的根；

当，即时，方程没有根。

知识点

直线和圆的方程的应用

继续学习学习下一知识点

下一知识点 : 圆方程的综合应用

百度题库 > 高考 > 理科数学 > 直线和圆的方程的应用

扫码查看完整答案与解析