- 匀速圆周运动
- 共72题
3.如图所示,一位高为h的中学生绕着O点把倒在地上的旗杆扶起来,当学生以速度v向左运动时,旗杆与地面的夹角恰为α,则旗杆转动的角速度为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,叠放在水平转台上的物体A、B、C能随转台一起以角速度ω匀速转动,A、B、C的质量分别为3m、2m、m,A与B、B和C与转台间的动摩擦因数都为μ,A 和B、C离转台中心的距离分别为r、1.5r 。设本题中的最大静摩擦力等于滑动摩擦力,下列说法正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.如图所示,有一内壁光滑的试管装有质量为1 g的小球,试管的开口端封闭后安装在水平轴O上,转动轴到管底小球的距离为5 cm,让试管在竖直平面内做匀速转动.问:
(1)转动轴达某一转速时,试管底部受到小球的压力的最大值为最小值的3倍,此时角速度ω1多大?
(2)当转动的角速度ω2=10 rad/s时,管底对小球的作用力的最大值和最小值各是多少?(g取10 m/s2)
正确答案
解析:(1)转至最低点时,小球对管底压力最大;转至最高点时,小球对管底压力最小,最低点时管底对小球的支持力F1应是最高点时管底对小球支持力F2的3倍,
即F1=3F2①
根据牛顿第二定律有
最低点:F1-mg=mrω12②
最高点:F2+mg=mrω12③
由①②③得ω1= 
(2)在最高点时,设小球不掉下来的最小角速度为ω0,
则mg=mrω02
ω0= 

因为ω2=10 rad/s<ω0=14.1 rad/s,
故管底转到最高点时,小球已离开管底,
因此管底对小球作用力的最小值为F′=0
当转到最低点时,管底对小球的作用力最大为F1′,
根据牛顿第二定律知F1′-mg=mrω22,
则F1′=mg+mrω22=1.5×10-2 N。
解析
解析已在路上飞奔,马上就到!
知识点
物体作匀速圆周运动,以下说法正确的是()
正确答案
解析
略
知识点
36.如图所示,质量为m1=0.01Kg的子弹A,垂直纸筒的旋转轴穿过高速旋转的纸筒B且只在B上留下一个弹孔,子弹穿过B后打入质量为m2=0.99Kg的木块C中,并在C里面(A、C可视为质点)。木块C放在长木板D的左端,D的质量m3=3kg,长度为L1=0.375m。长木板刚在光滑的水平桌面上,水平桌面的右端有一很薄的与D等高的固定挡板E,D的右端到E距离L2=0.125m,D碰到即被粘牢,C则离开D飞到桌面下方的水平地面上。已知纸筒直径d=30cm,纸筒匀速旋转的角速度

(1)若发生子弹的枪有两个档位,可以发射两种初速度不同的子弹,为了让子弹穿过纸筒的时间尽可能短,子弹两个档位的速度大小分别是多少?
(2)在(1)问中,讨论子弹打入C后,整体能否与D达到共同速度,并求出AC整体能与D达到共速情况下AC整体落到地面上距桌边的距离。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.在街头的理发店门口,常可以看到这样的标志:一个转动的圆筒,外表有彩色螺旋斜条纹,我们感觉条纹在沿竖直方向运动,但实际上条纹在竖直方向并没有升降,这是由于圆筒的转动而使我们的眼睛产生的错觉,如图所示,假设圆筒上的条纹是围绕圆筒的一条宽带,相邻两圈条纹在沿圆筒轴线方向的距离(即螺距)为L,如果我们观察到条纹以速度v向上运动,则圆筒的转动情况是( )(从上往下看)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
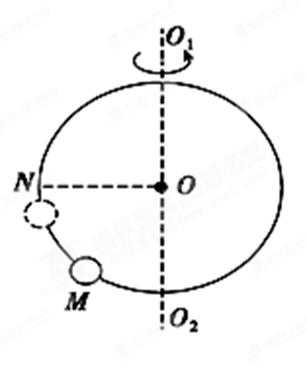
18.如图所示,光滑圆环可绕竖直轴O1O2旋转,在圆环上套一个小球,实验时发现,增大圆环转速,小球在圆环上的位置升高,但无论圆环转速多大,小球都不能上升到与圆心O等高的N点.现让小球带上正电荷,下列措施可以让小球上升到N点的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.
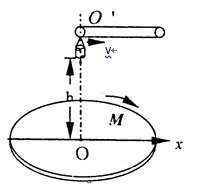
如图所示,M是水平放置的半径足够大的圆盘, 绕过其圆心的竖直轴OO′匀速转动,以经过O水平向右的方向作为x轴的正方向。在圆心O正上方距盘面高为h处有一个正在间断滴水的容器挂在传送带下面,在t=0时刻开始随传送带沿与x轴平行的方向做匀速直线运动,速度大小为v。已知容器在t=0时滴下第一滴水,以后每当前一滴水刚好落到盘面上时再滴一滴水。求:
(1)每一滴水经多长时间滴落到盘面上?
(2)要使每一滴水在盘面上的落点都位于一条直线上,圆盘转动的最小角速度ω。
(3)第二滴水与第三滴水在盘面上的落点间的最大距离s。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
24.如图所示,M是水平放置的半径足够大的圆盘,可绕过其圆心的竖直轴OO’匀速转动,在圆心O正上方h处有一个正在间断滴水的容器,每当一滴水落在盘面时恰好下一滴水离开滴口。某次一滴水离开滴口时,容器恰好开始水平向右做速度为v的匀速直线运动,将此滴水记作第一滴水。不计空气阻力,重力加速度为g。求:
(1)相邻两滴水下落的时间间隔;
(2)要使每一滴水在盘面上的落点都在一条直线上,求圆盘转动的角速度。
(3)第二滴和第三滴水在盘面上落点之间的距离最大可为多少?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析