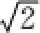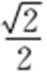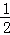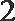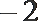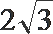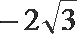- 平面向量
- 共1072题
8．若点
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
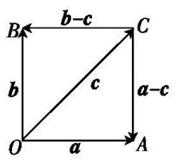
5.已知a，b是平面内两个互相垂直的单位向量，若向量c满足(a-c)·(b-c)=0，则|c|的最大值是（ ）
A1
B2
C
D
正确答案
解析
因为(a-c)·(b-c)=0，所以(a-c)⊥(b-c).
如图所示，设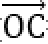
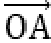
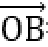
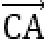
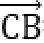
又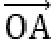
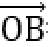
当且仅当OC为圆的直径时，|c|最大，且最大值为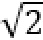
知识点
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
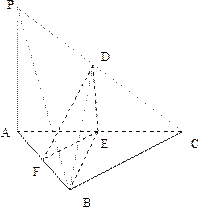
如图，在三棱锥P
求证：（1）直线PA∥平面DEF;
（2）平面BDE⊥平面ABC.
正确答案
见解析。
解析
（1）∵D,E,分别为PC,AC,的中点
∴DE∥PA
又∵DE 
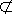
∴直线PA∥平面DEF
（2）∵E,F分别为棱AC,AB的中点，且BC=8，由中位线知EF=4
∵D,E,分别为PC,AC,的中点，且PA=6，由中位线知DE=3，又∵DF=5
∴DF²=EF²+DE²=25，∴DE⊥EF，又∵DE∥PA，∴PA⊥EF，又∵PA⊥AC，又∵AC 
AC 
∴平面BDE⊥平面ABC
知识点
设函数f（x），g（x）的定义域都为R，且f（x）是奇函数，g（x）是偶函数，则下列结论中正确的是（ ）
正确答案
解析
f（x）是奇函数，g（x）是偶函数，∴|f（x）|为偶函数，|g（x）|为偶函数。
再根据两个奇函数的积是偶函数、两个偶函数的积还是偶函数、一个奇函数与一个偶函数的积是奇函数，
可得 f（x）|g（x）|为奇函数，
知识点
设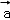
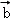
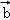
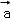
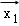
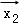
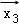
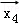
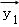
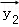
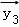
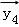
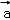
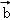
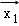
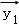
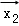
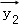
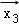
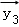
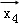
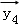
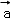
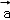
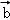
A
B
C
D0
正确答案
解析
由题意，设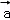
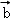
分类讨论可得
①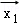
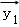
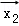
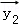
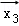
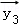
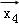
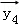
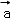
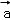
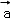
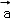
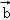
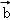
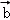
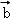
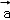
②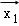
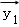
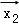
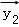
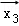
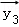
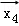
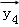
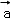
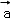
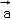
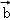
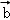
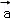
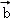
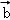
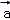
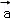
③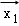
∴
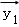
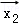
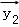
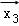
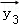
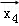
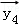
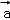
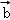
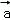
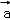
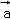
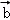
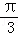
知识点
已知函数
（1）当
（2）若
正确答案
见解析。
解析
（1）当
令
所以当
（2)
令
所以，在区间
在区间
又易知
①当
②当
③当
综上，
知识点
复数（3+2i）i等于（ ）
正确答案
解析
（3+2i）i=3i+2i2=﹣2+3i。
知识点
1.设集合A={x|
正确答案
解析
化简集合A=[-2.2]，B=[0,+
考查方向
解题思路
化简集合A,B, 然后求交集.
易错点
问题容易忽略元素特征出错,认为是抛物线与双曲线的交点坐标,所以选择D
知识点
8.若a，b，c均为单位向量，且a·b=0，(a－c)·(b－c)≤0，则|a+b－c|的最大值为（ ）
A
B1
C
D2
正确答案
解析
设a=(1，0)，b=(0，1)，c=(x，y)，则x2+y2=1，
a－c=(1－x，－y)，b－c=(－x，1－y)，
则(a－c)·(b－c)=(1－x)(－x)+(－y)(1－y)=x2+y2－x－y=1－x－y≤0，即x+y≥1，
又a+b－c=(1－x，1－y)，
∴|a+b－c|=
∵c=(x，y)对应的点在
∴|a+b－c|的最大值为1.
知识点
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
设x∈R，向量a＝(x,1)，b＝(1，－2)，且a⊥b，则|a＋b|＝
( )
A
B
C
D10
正确答案
解析
因为a⊥b，所以a·b＝x－2＝0，解得x＝2，a＝(2,1)，a＋b＝(3，－1)，|a＋b|＝
知识点
9.称
A
B
C
D
正确答案
解析
如图：
∵|
用
∴d（
|
知识点
4.已知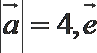
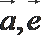
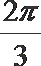
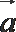
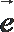
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
扫码查看完整答案与解析