- 平面向量
- 共1072题
15．已知平面向量a，b，|a|=1，|b|=2，a·b=1．若e为平面单位向量，则|a·e|+|b·e|的最大值是______．
正确答案
知识点
13.已知向量a=(m,4)，b=(3,-2)，且a∥b，则m=___________.
正确答案
-6
知识点
14．在平面直角坐标系
正确答案
解析
在同一直角坐标系内，作出
由题意，可知
考查方向
解题思路
先根据题意作出函数的大致图象，然后根据图像判断
易错点
数形结合思想运用不好，不会想到作图
知识点
13.已知向量a=(m,4)，b=(3,-2)，且a∥b，则m=___________.
正确答案
-6
知识点
2.设向量a＝(2，4)与向量b＝(x，6)共线，则实数x＝( )
A2
B3
C4
D6
正确答案
解析
由向量平行的性质有
考查方向
解题思路
直接根据向量共线的充要条件求解既可。
易错点
将向量共线和垂直的充要条件混淆，导致出错。
知识点
9. 已知抛物线C：
A3
B6
C
D
正确答案
解析
直线PF的方程为y=x-2，与抛物线方程联立，解得x=4,所以
考查方向
解题思路
本题考查抛物线的简单几何性质，解题步骤如下：1、由题可知，易得直线PF的方程。2、将直线方程与抛物线联立，解得
易错点
本题易在求解时把分母平方运算。
知识点
2.若平面向量a=(m,1)，b=(2,1)，且(a-2b)//b，则m =（ ）
正确答案
解析
因为a-2b =（m-4,-1）, b=(2,1)且(a-2b)//b，所以m-4= -2, 则m=2.
考查方向
解题思路
把向量a-2b的坐标表示出来，根据两个向量平行公式，建立关于m的方程， 即可求出m的值。
易错点
向量的平行或垂直的公式容易弄混淆。
知识点
3.已知非零向量
A
B或
C
D
正确答案
解析
因为两向量平行，所以
考查方向
平面向量的数量积
向量的平行关系
解题思路
根据向量平行的性质，求解出m的值
易错点
计算错误，向量平行的数量积计算错误
知识点
3. 若
A
B
C
D
正确答案
解析
因为
考查方向
解题思路
根据向量平行时数量积的特点进行求解
易错点
混淆向量平行和向量垂直时，向量数量积不同。
知识点
3．已知向量a=(2，x)．b=（一4，2）．若（a十b）∥(2a-b)，则实数x的值为（ ）
正确答案
解析
试题分析：本题属于平面向量中的基本问题，题目的难度是简单。
考查方向
本题主要考查了平面向量的平行的坐标表示,在近几年的各省高考题出现的频率较高。
解题思路
本题考查平面向量的位置关系，解题步骤如下：
（1）由题可知，易得a+b=(-2,x+2),2a-b=(8,2x-2)。
（2）令8(x+2)=-2(2x-2)，解得x= -1.
易错点
本题易在应用平行的坐标表示公式时发生错误。
知识点
4.若
A
B
C
D
正确答案
解析
因为A B C D四点共线，所以AB和CD平行，所以
考查方向
向量运算
解题思路
根据向量共线，建立等量关系，求出t的值
易错点
计算错误，对向量的数量积性质混淆
知识点
《安全生产法》对安全生产监督检查人员履行职责提出的要求包括( )。
A．忠于职守，坚持原则，秉公执法
B．执行监督检查任务时，必须出示有效的监督执法证件
C．不准为生产经营单位提供技术咨询服务
D．必须严格按照程序履行职责，规范执法，保守秘密
E．履行监督检查职责不得影响被检查单位的正常生产经营活动
正确答案
A,B,D,E
解析
暂无解析
函数
正确答案
解析
根据韪得：
知识点
在平面直角坐标系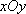
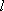
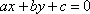
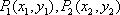
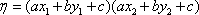
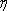
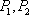
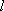
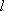
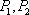
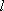
⑴ 求证：点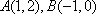
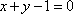
⑵ 若直线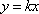
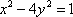
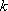
⑶ 动点M到点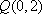
正确答案
见解析。
解析
（1）证明：因为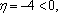
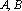
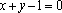
（2）解：直线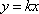
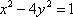
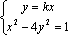
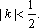
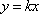
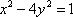
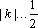
当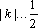
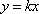
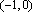
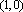
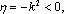
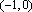
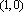
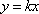
故实数
（3）证明：设M的坐标为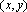
则曲线E的方程为
对任意的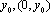
又曲线E上的点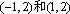
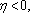
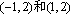
所以y轴为曲线E的分割线。
知识点
设△ABC的内角A，B，C所对边的长分别为a，b，c，且b=3，c=1，△ABC的面积为
正确答案
见解析
解析
∵b=3，c=1，△ABC的面积为
∴
∴sinA=
又∵sin2A+cos2A=1
∴cosA=±
由余弦定理可得a=
知识点
扫码查看完整答案与解析