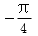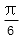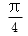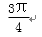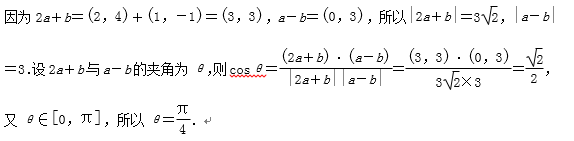- 平面向量
- 共1072题
设




正确答案
解析
依题意,对任意实数




知识点
设e1,e2为单位向量,非零向量b=xe1+ye2,x,y∈R.若e1,e2的夹角为

正确答案
2
解析
因为b≠0,所以b=xe1+ye2,x≠0,y≠0.
又|b|2=(xe1+ye2)2=x2+y2+








知识点
若非零向量


正确答案
解析
略。
知识点
已知向量


正确答案
解析
略
知识点
若向量a=(1,2),b=(1,-1),则2a+b与a-b的夹角等于( )
正确答案
解析
知识点
在


正确答案
解析
略
知识点
已知单位向量e1,e2的夹角为60°,则|2e1-e2|=________.
正确答案
解析
知识点
命题











正确答案
解析
命题







知识点
平面向量





正确答案
解析
略
知识点
正确答案
(1) 
(2)
解析
知识点
向量



(1)求函数
(2)已知锐角






正确答案
见解析。
解析
(1)由
即
函数
(2)由

∵
∴
由正弦定理:

得
又∵
即
∴
知识点
由空间向量




正确答案
解析
略
知识点
已知非零向量




正确答案
解析
略
知识点
已知两不共线向量

正确答案
解析
略
知识点
平面向量a与b的夹角为



正确答案
解析
略
知识点
扫码查看完整答案与解析