- 平面向量
- 共1072题
4.向量


正确答案
解析
由










考查方向
解题思路
先根据题意得到

易错点
不会根据

知识点
4.已知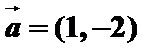
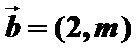
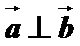
正确答案
解析
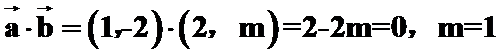
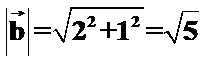
考查方向
解题思路
先根据垂直数量积为零求出未知参数m,再计算出b向量的模。
易错点
本题不知道向量垂直坐标满足的关系式 。
知识点
4.已知

正确答案
解析


考查方向
解题思路
先将要求的模平方,利用2个向量是单位向量并且垂直即可算出。
易错点
向量的求模方法忘记。
知识点
14.已知|






正确答案
解析
因为

考查方向
解题思路
先根据向量的数量积的定义,再根据向量垂直的性质求λ的值
易错点
平面向量及其应用
知识点
14.已知|






正确答案
解析
由题意可得
再根据向量

求得
故答案为
考查方向
解题思路
由题意利用两个向量的数量积的定义求得
再根据向量


易错点
两个向量垂直,数量积为0.
知识点
13.设向量a=(x,x+1),b=(1,2),且a⊥b,则x= .
正确答案
1
知识点
若向量





正确答案
解析
设





∴


∴
∴

∴
知识点
设向量









正确答案
解析
∵|













两式相减得4



知识点








正确答案
解析
由





知识点
5. 已知向量



A .
正确答案
解析




考查方向
解题思路
利用向量垂直的条件:两向量数量积为零,利用向量坐标运算求数量积
易错点
熟悉向量数量积的坐标运算,向量垂直的条件。
知识点
在四边形

正确答案
解析
本题考查的是向量垂直的判断以及向量的模长,因为


知识点
已知













(1)证明:点

(2)设点






正确答案
见解析。
解析
(1)




设
则
由题意得
所以点

经验证点




(2)由




设





由①、②得







故 
又 

所以 
由此知





(2)法二:
同理
所以
因此A、P、B、Q四点在同一圆上。
知识点
已知


(1)若
(2)求
正确答案
(1)

解析
(1)解:由题意知焦点
设



由

(2)解:设直线

由
于是
所以

由
所以

由
又因为
点

所以
记
令
可得



又
所以,当


所以,
知识点
已知向量



正确答案
解析
知识点
在平面直角坐标系




正确答案
5
解析
知识点
扫码查看完整答案与解析