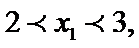- 指数函数与对数函数的关系
- 共10题
8.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.当


正确答案
解析
假定
则切线方程为
因为过原点,得
而
所以
从而
那么
(1) 当

故函数

(2) 当

故函数

(3) 当
故函数

于是,正确的答案为A.
知识点
14.设a > 1,函数
(1)求

(2) 若
(3)若
正确答案
解:
(1) 由
∴
∴
(2) ∵ a > 1 ∴ 
∴ 
∴ 
∴
(3)
要使
只需
∴
∴
因此,a的取值范围为
解析
解析已在路上飞奔,马上就到!
知识点
14.已知




正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
5.若函数




正确答案
解析
∵函数


∴以




∴所求解析式为
考查方向
本题考查函数的图像变换,是容易题.
解题思路
函数









易错点
混淆各种函数图像变换.
知识点
16.设函数




正确答案
2
解析
设








考查方向
解题思路
本题考查函数图象的对称性,解题步骤如下:
法—:
1、由点


2、所以设



法二:
由点





易错点
1、本题易在解题思路上受阻。
2、点关于线对称的计算上和指数运算上。
知识点
12.已知
正确答案
解析
我们首先可以用图象法来解:如图,在同一坐标系中作出四个函数,
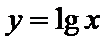
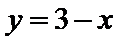

设
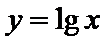
其横坐标为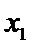
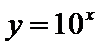
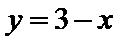
其横坐标为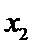
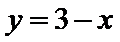

其横坐标为
因为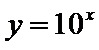
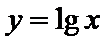

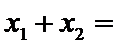
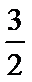
考查方向
解题思路
此属于数形结合法。现在用估计法来解它:因为
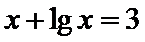
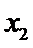
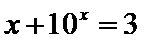
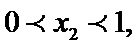
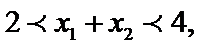
易错点
易忽略函数的对称性,以及指对数函数成反函数的关系
知识点
3.已知函数


正确答案
1
解析
因为原函数的函数值与自变量分别是反函数的自变量与函数值,所以原题等价于求

考查方向
解题思路
本题考查反函数的概念以及转化与化归的数学思想,解题思路如下:利用反函数的定义,求

易错点
本题必须注意原函数的函数值与自变量分别是反函数的自变量与函数值,忽视则会出现错误或者导致运算复杂。
知识点
扫码查看完整答案与解析