- 函数的图象与图象变化
- 共172题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
某企业有甲、乙两个研发小组,为了比较他们的研发水平,现随机抽取这两个小组往年研发新产品的结果如下:
(a,b),(a,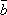
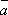
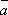
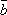
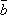
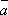

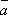

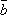

其中a,
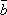
(1)若某组成功研发一种新产品,则给该组记1分,否则记0分,试计算甲、乙两组研发新产品的成绩的平均数和方差,并比较甲、乙两组的研发水平;
(2)若该企业安排甲、乙两组各自研发一种新产品,试估计恰有一组研发成功的概率。
正确答案
见解析。
解析
(1)甲组研发新产品的成绩为1,1,1,0,0,1,1,1,0,1,0,1,1,0,1,
其平均数为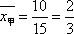
方差为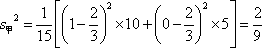
乙组研发新产品的成绩为1,0,1,1,0,1,1,0,1,0,0,1,0,1,1,
其平均数为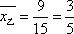
方差为
因为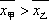
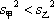
所以甲组的研发水平优于乙组。
(2)记E={恰有一组研发成功}。
在所抽得的15个结果中,恰有一组研发成功的结果是(a,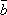
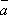
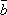
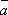
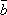
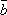
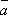
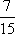
将频率视为概率,即得所求概率为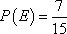
在第(1)问中,通过已知条件可分别写出甲、乙两组的成绩,然后利用平均数公式分别计算甲、乙两组的平均成绩,再结合方差公式得到甲、乙两组的方差,进而比较甲、乙两组的研发水平;在第(2)问中,充分利用古典概型的概率公式,转化为计算基本事件的个数,从而求得概率。
知识点
直线

正确答案
解析
涉及到的是直线和圆的知识,由于北京的考卷多年没有涉及直线和圆,对于考生来说,可能有些陌生,直线和圆相交求弦长,利用直角三角形解题,也并非难题。将题目所给的直线和圆图形化得到如右图所示的情况,半弦长 



知识点
平面上一机器人在行进中始终保持与点F(1,0)的距离和到直线x=-1的距离相等,若机器人接触不到过点P(-1,0)且斜率为k的直线,则k的取值范围是__________。
正确答案
(-∞,-1)∪(1,+∞)
解析
由题意知,机器人行进的路线为抛物线y2=4x.由题意知过点P的直线为y=kx+k(k≠0),要使机器人接触不到过点P的直线,则直线与抛物线无公共点,联立方程得
知识点
正确答案
解析
因为




知识点
扫码查看完整答案与解析






