函数的图象与图象变化
共172题

· 函数的图象与图象变化

函数的图象与图象变化
共172题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

小明骑车上学，开始时匀速行驶，途中因交通堵塞停留了一段时间，后为了赶时间加快速度行驶. 与以上事件吻合得最好的图象是（）

正确答案

解析

可以将小明骑车上学的行程分为三段，第一段是匀速行驶，运动方程是一次函数，即小明距学校的距离是他骑行时间的一次函数，所对应的函数图象是一条直线段，由此可以判断A是错误的；第二段因交通拥堵停留了一段时间，这段时间内小明距学校的距离没有改变，即小明距学校的距离是行驶时间的常值函数，所对应的函数图象是平行于x轴的一条线段，由此可以排除D；第三段小明为了赶时间加快速度行驶，即小明在第三段的行驶速度大于第一段的行驶速度，所以第三段所对应的函数图象不与第一段的平行，从而排除B. 故选C.

知识点

函数的图象与图象变化

题型：单选题

单选题 · 5 分

已知函数是定义在R上的奇函数，且满足当时，，则使的的值是（）

正确答案

解析

略。

知识点

函数的图象与图象变化

题型：单选题

单选题 · 5 分

已知函数f(x)＝x3＋ax2＋bx＋c，下列结论中错误的是(　　)。

A∃x0∈R，f(x0)＝0

B函数y＝f(x)的图像是中心对称图形

C若x0是f(x)的极小值点，则f(x)在区间(－∞，x0)单调递减

D若x0是f(x)的极值点，则f′(x0)＝0

正确答案

解析

若x0是f(x)的极小值点，则y＝f(x)的图像大致如下图所示，则在(－∞，x0)上不单调，故C不正确，

知识点

函数的图象与图象变化

题型：单选题

单选题 · 5 分

已知且函数恰有3个不同的零点，则实数a的取值范围是（）

A[-1，+）

B[-1，0）

C（0，+ ）

D[-2，+ ）

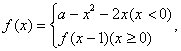
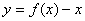
正确答案

解析

略。

知识点

函数的图象与图象变化

题型：简答题

简答题 · 14 分

已知函数。

（1）若，求曲线在点处的切线方程；

（2）求函数的单调区间；

（3）设函数，若至少存在一个，使得成立，求实数的取值范围。

正确答案

见解析。

解析

函数的定义域为，

。

（1）当时，函数，，。

所以曲线在点处的切线方程为，

即。

（2）函数的定义域为。

（i）当时，在上恒成立，

则在上恒成立，此时在上单调递减。

（ii）当时，，

（ⅰ）若，

由，即，得或；

由，即，得，

所以函数的单调递增区间为和，

单调递减区间为。

（ⅱ）若，在上恒成立，则在上恒成立，此时在上单调递增。

（3）因为存在一个使得，

则，等价于.

令，等价于“当时，”.

对求导，得.

因为当时，，所以在上单调递增.

所以，因此.

另解：

设，定义域为，.

依题意，至少存在一个，使得成立，

等价于当时，.

（1）当时，

在恒成立，所以在单调递减，

只要，则不满足题意.

（2）当时，令得.

（ⅰ）当，即时，

在上，所以在上单调递增，所以，

由得，，所以.

（ⅱ）当，即时，

在上，所以在单调递减，所以，

由得.

（ⅲ）当，即时，在上，在上，

所以在单调递减，在单调递增，

，等价于或，解得，所以，.

综上所述，实数的取值范围为.

知识点

函数的图象与图象变化

继续学习学习下一知识点

下一知识点 : 函数解析式的求解及常用方法

百度题库 > 高考 > 文科数学 > 函数的图象与图象变化

扫码查看完整答案与解析