- 平面与平面垂直的判定与性质
- 共129题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形。
(1)求该椭圆的离心率和标准方程;
(2)过B1作直线交椭圆于P,Q两点,使PB2⊥QB2,求△PB2Q的面积。
正确答案
(1) 
解析
(1)
如图,设所求椭圆的标准方程为
因△AB1B2是直角三角形,又|AB1|=|AB2|,故∠B1AB2为直角,因此|OA|=|OB2|,得

在Rt△AB1B2中,OA⊥B1B2,故


由题设条件
因此所求椭圆的标准方程为
(2)由(1)知B1(-2,0),B2(2,0),由题意,直线PQ的倾斜角不为0,故可设直线PQ的方程为x=my-2.代入椭圆方程得
(m2+5)y2-4my-16=0.(*)
设P(x1,y1),Q(x2,y2),则y1,y2是上面方程的两根,因此

又

所以

=(my1-4)(my2-4)+y1y2
=(m2+1)y1y2-4m(y1+y2)+16
=
=
由PB2⊥QB2,知

解得m=±2.
当m=2时,方程(*)化为9y2-8y-16=0,
故


△PB2Q的面积S=

当m=-2时,同理可得(或由对称性可得)△PB2Q的面积
综上所述,△PB2Q的面积为
知识点
如图,在直三棱柱
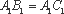

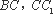


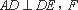

求证:(1)平面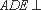
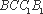
(2)直线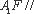

正确答案
见解析
解析
(1)∵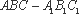

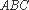
又∵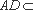
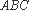
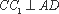
又∵
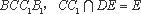
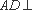
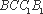
又∵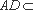
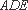
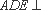
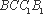
(2)∵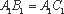
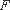
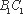
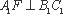
又∵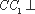
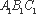
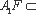
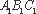
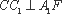
又∵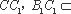

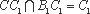
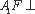
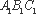
由(1)知,
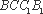
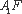
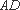
又∵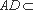
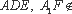
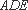

知识点
如图,在四棱锥A—BCDE中,平面





(1)证明:

(2)求直线
正确答案
见解析
解析
证明:(1)连接



由

又平面


(2)在直角梯形


又平面


做








在


在


在


所以,直线

知识点
如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥平面ABCD,PA⊥AD.E和F分别是CD和PC的中点。
求证:
(1)PA⊥底面ABCD;
(2)BE∥平面PAD;
(3)平面BEF⊥平面PCD.
正确答案
见解析
解析
(1)因为平面PAD⊥底面ABCD,且PA垂直于这两个平面的交线AD,
所以PA⊥底面ABCD.
(2)因为AB∥CD,CD=2AB,E为CD的中点,
所以AB∥DE,且AB=DE.
所以ABED为平行四边形。
所以BE∥AD.
又因为BE

所以BE∥平面PAD.
(3)因为AB⊥AD,而且ABED为平行四边形,
所以BE⊥CD,AD⊥CD.
由(1)知PA⊥底面ABCD,所以PA⊥CD.
所以CD⊥平面PAD.所以CD⊥PD.
因为E和F分别是CD和PC的中点,
所以PD∥EF.所以CD⊥EF.
所以CD⊥平面BEF.
所以平面BEF⊥平面PCD.
知识点
(x+2)8的展开式中x6的系数是( )。
正确答案
解析
T2+1=
知识点
如图,四棱锥




(1)求证:
(2)求证:
正确答案
见解析。
解析
知识点
将长方体截去一个四棱锥,得到的几何体如右图所示,则该几何体的左视图为( )
正确答案
解析
左视图即是从正左方看,找特殊位置的可视点,连起来就可以得到答案。
知识点
设a,b是两个非零向量,( )
正确答案
解析
由|a+b|=|a|-|b|两边平方可得,|a|2+2a·b+|b|2=|a|2-2|a||b|+|b|2,即a·b=-|a||b|,所以cos〈a,b〉=-1,即a与b反向,根据向量共线定理,知存在实数λ,使得b=λa
知识点
下列函数中,满足“f(x+y)=f(x)f(y)”的单调递增函数是( )
正确答案
解析
A)f(x)=x3,f(y)=y3,f(x+y)=(x+y)3,不满足f(x+y)=f(x)f(y),故A错;
B)f(x)=3x,f(y)=3y,f(x+y)=3x+y,满足f(x+y)=f(x)f(y),且f(x)在R上是单调增函数,故B正确;
C)f(x)=


D)f(x)=


知识点
扫码查看完整答案与解析