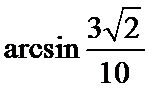- 直线与平面垂直的判定与性质
- 共118题
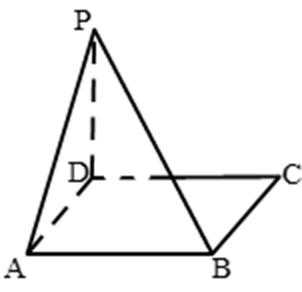
19.如图,在四棱锥P-ABCD的底面是边长为2的正方形,PD⊥平面ABCD, E、F分别是PB、AD的中点,PD=2.
(I)求证:BC⊥PC;
(II)求证:EF//平面PDC;
(III)求三棱锥B—AEF的体积.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
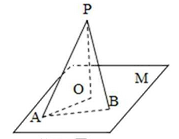
19.如图,在三棱锥P—ABC中,
(I)求证:
(II)求点A到平面PEF的距离;
(III)求二面角E—PF—A的正切值。
正确答案
: 解法一:
(I)
AD为PD在平面ABC内的射影。
又
在


(II)设EF与AD相交于点G,连接PG。


过A做AO
所以线段AO的长为点A到平面PEF的距离
在
即点A到平面PEF的距离为
说 明:该问还可以用等体积转化法求解,请根据解答给分。
(III)

过A做
则
所以
在
即二面角E—PF—A的正切值为
解法二:

则A(0,0,0),E(2,0,0),D(2,2,0),F(0,2,0),P(0,0,2)
(I)
且

(II)
则
令
故点A到平面PEF的距离
所以点A到平面PEF的距离为
(III)依题意
设二面角E—PF—A的大小为

则,
所以
即二面角E—PF—A的正切值为
解析
解析已在路上飞奔,马上就到!
知识点
4. 已知平面


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 如图,在三棱柱










(1)证明:
(2)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 如图,直线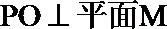

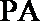
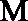
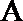
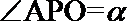
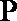
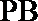

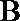
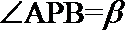
①若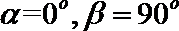
②若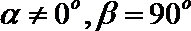
③若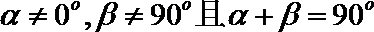
④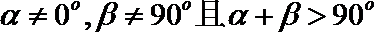
⑤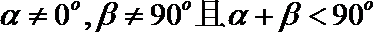
正确答案
②③
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,四棱锥





(I)证明:

(II)设





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.设

①若



②若




③设



④直线


其中所有的真命题的序号是__________ .
正确答案
①②
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,







(1)求证:
(2)设


(3)设平面


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知在四棱锥P - ABCD中,底面 ABCD是矩形,
(1)求证:AF
(2)求三棱锥B-PEC的体积;
(3)求证:AF//平面PEC
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.如图,已知边长为6的正方形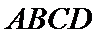
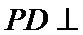
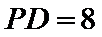
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析