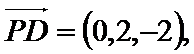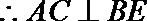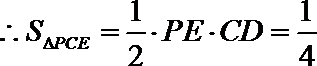- 直线与平面垂直的判定与性质
- 共118题
19.如图,四棱锥P﹣ABCD,PA⊥底面ABCD,AB∥CD,AB⊥AD,AB=AD=
(Ⅰ) 证明:EF∥平面PAB;
(Ⅱ) 求直线AC与平面ABEF所成角的正弦值.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.如图所示,三棱锥







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.如图,在等腰梯形













正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.如图,在四棱锥









(1)证明:直线
(2)求异面直线

正确答案
方法一(综合法)
(1)取OB中点E,连接ME,NE
又
(2)



连接

所以 

方法二(向量法)作
如图,分别以AB,AP,AO所在直线为

(1)
设平面OCD的法向量为

即

(2)设





解析
解析已在路上飞奔,马上就到!
知识点
19. 如图,在三棱锥A—BOC中,


(I)求证:
(II)在线段CB上是否存在一点F,使得在CO上任取一点G均有AG//平面DEF?若存在,试确定F的位置;若不存在,请说明理由.
正确答案
(I)证明:因为

因为OB=OC=1,BC=2,所以

因为AO与BO相交于点O,所以CO垂直于平面AOB。
(II)适合条件的点F在在,且F是BC的中点,证明如下:
取BC的中点F,连结DF、EF。
因为D是OB的中点,所以DF//OC,同理,EF//AC,所以平面DEF//平面AOC。
因为AG在平面AOC内,所以AG//平面DEF。
解析
解析已在路上飞奔,马上就到!
知识点
17.如图所示,矩形








(1)求证:

(2)求证:

(3)求三棱锥
正确答案
(1)略;
(2)略;
(3)
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,在四棱锥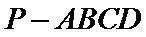


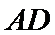

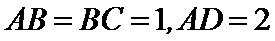
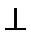


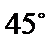

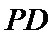
(Ⅰ)求证: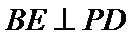
(Ⅱ)求二面角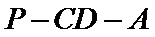
正确答案
解:
解法二:(1) 如图,建立空间直角坐标系,由已知可得:余弦
A(0,0,0), B(1,0,0),C(1,1,0),
D(0,2,0), P(0,0,2), E(0,1,1),
(2)
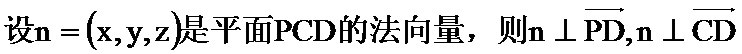
由
得
令y=1,则n=(1,1,1),
所以,所求二面角的余弦值为
解析
解析已在路上飞奔,马上就到!
知识点
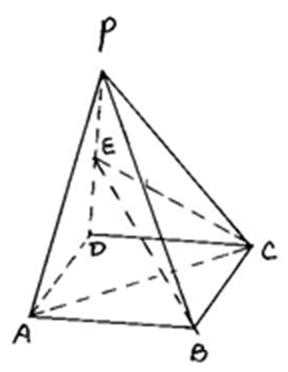
17.如图,四棱锥P-ABCD的底面是正方形,PD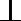
(1)求证:AC
(2)若PD=AD=1,且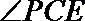
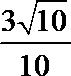
正确答案
解:(1)连接BD 
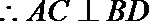
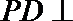

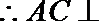
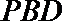
又BE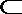
(2)设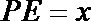
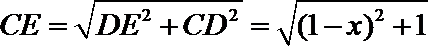
又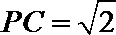
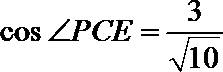

解析
解析已在路上飞奔,马上就到!
知识点
16.如图,在四棱锥










求证:
(1)

(2)

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设a,b为两条不同的直线,α,β为两个不重合的平面。下列命题中正确的是( )
正确答案
解析
选项A中,a可以包含于β,A错误;选项B中,a与b可以异面,B错误;选项C中,α与β可以相交。故选D。
知识点
扫码查看完整答案与解析