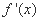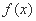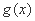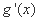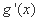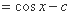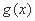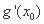- 函数性质的综合应用
- 共80题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知函数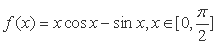
(1)求证: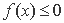
(2)若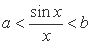
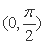
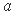
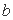
正确答案
见解析。
解析
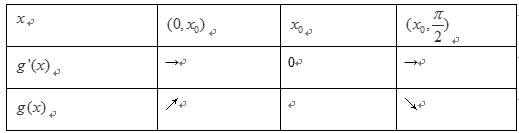
(1)由

因为在区间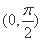
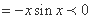
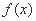
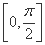
从而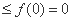
(2)当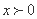
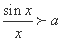
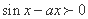
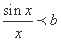
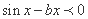
令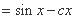
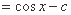
当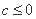
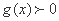
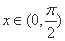
当
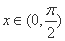
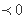
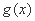
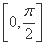
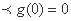
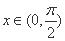
当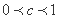
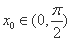
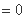
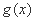
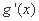
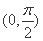
因为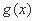
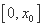
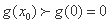

任意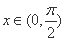
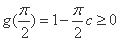
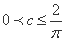
综上所述,当且仅当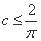
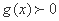
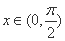
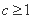
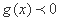
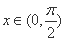
所以,若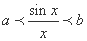
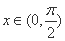

知识点
已知











(1)当


(2)设












正确答案
见解析。
解析
知识点
设函数












正确答案
解析
无论





即



画出这两个图象可以看出


知识点
已知

①


②对任意不同的

那么,关于


正确答案
解析
令
则

又因为









知识点
若函数





给出下列四个函数:①



其中具有性质M的函数是 (注:把满足题意的所有函数的序号都填上)
正确答案
①、③
解析
可通过作差比较得到结论.
知识点
20.函数





(1)求

(2)求

(3)若函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 设函数
①

②

③

④方程
上述命题中的所有正确命题的序号是_________.
正确答案
①②③
解析
解析已在路上飞奔,马上就到!
知识点
7.对于函数:
①
②
③
判断如下三个命题的真假:
命题甲:
命题乙:


命题丙:

能使命题甲、乙、丙均为真的所有函数的序号是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析