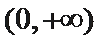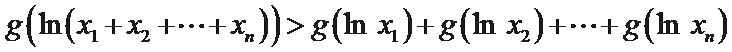- 函数性质的综合应用
- 共80题
14. 若对于函数
①b=0时,
②y=
③b=-1时,方程
④b=-1时,不等式
其中正确的命题是______.(写出所有正确命题的编号)
正确答案
①②④
解析
解析已在路上飞奔,马上就到!
知识点
12.设函数
①当c=0时,有
②当b=0,c>0时,方程
③函数
④当x>0时;函数


其中正确的命题的序号是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.给出下列几个命题:
①若函数


②若函数





③已知




④设函数



⑤若



其中正确的命题序号是___________.(写出所有正确命题的序号)
正确答案
①④⑤
解析
解析已在路上飞奔,马上就到!
知识点
16.定义






①函数


②方程
③函数
④关于实数

其中你认为正确的所有命题的序号为
正确答案
②③④
解析
解析已在路上飞奔,马上就到!
知识点
14.函数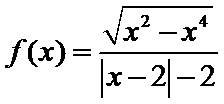
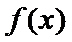
①函数的定义域和值域均为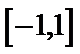
②函数的图像关于原点成中心对称;
③函数在定义域上单调递增;
④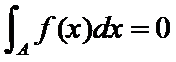
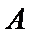
⑤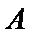
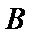
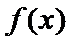
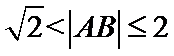
请写出所有关于函数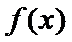
正确答案
②④
解析
解析已在路上飞奔,马上就到!
知识点
6.已知下列三组条件:
(1)

(2)


(3)






其中

正确答案
(1)(2)
解析
解析已在路上飞奔,马上就到!
知识点
3.下列命题中是假命题的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.符号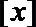
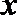
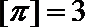
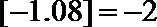

①函数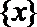
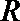
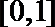
②方程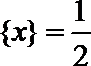
③函数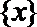
④函数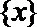
其中正确命题的序号有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.对于函数f(x)(x∈D),若x∈D时,恒有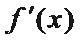
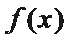
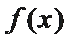
(Ⅰ)当函数f(x)=m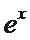
(Ⅱ)若函数g(x)为(0,+∞)上的J函数,试比较g(a)与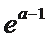
正确答案
解:(Ⅰ)由
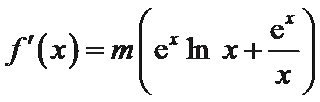
因为函数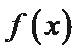
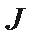
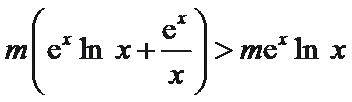
即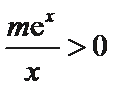
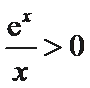
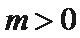
即
(Ⅱ)①构造函数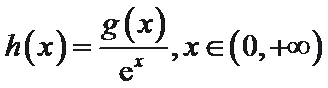
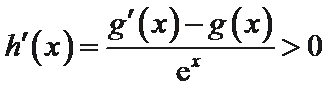
可得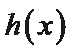
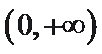
当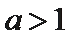
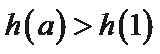
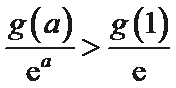
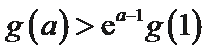
当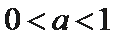
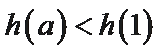
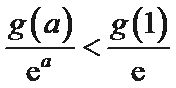
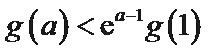
当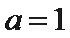
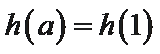
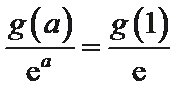
②因为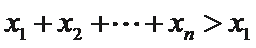
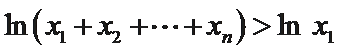
由①可知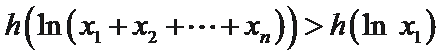

整理得
同理可得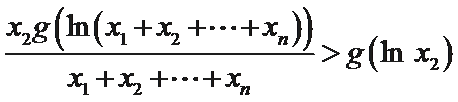
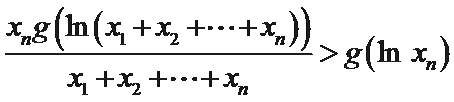
把上面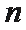
可得
解析
解析已在路上飞奔,马上就到!
知识点
18.若



①

②

③


④函数


则以上各命题中正确的个数是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析