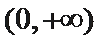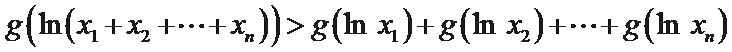- 函数性质的综合应用
- 共80题
1
题型:填空题
|
6.已知下列三组条件:
(1)

(2)


(3)






其中

正确答案
(1)(2)
解析
解析已在路上飞奔,马上就到!
知识点
充要条件的判定函数性质的综合应用
1
题型:
单选题
|
3.下列命题中是假命题的是( )
正确答案
A
解析
解析已在路上飞奔,马上就到!
知识点
命题的真假判断与应用函数性质的综合应用
1
题型:
单选题
|
8.符号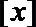
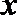
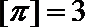
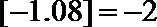

①函数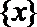
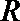
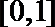
②方程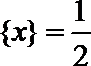
③函数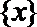
④函数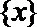
其中正确命题的序号有( )
正确答案
A
解析
解析已在路上飞奔,马上就到!
知识点
命题的真假判断与应用函数性质的综合应用
1
题型:简答题
|
21.对于函数f(x)(x∈D),若x∈D时,恒有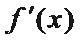
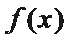
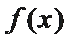
(Ⅰ)当函数f(x)=m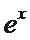
(Ⅱ)若函数g(x)为(0,+∞)上的J函数,试比较g(a)与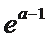
正确答案
解:(Ⅰ)由
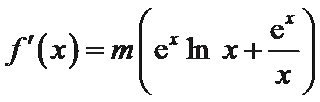
因为函数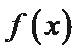
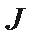
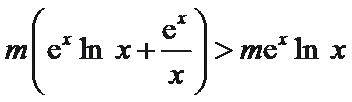
即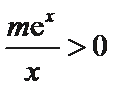
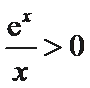
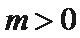
即
(Ⅱ)①构造函数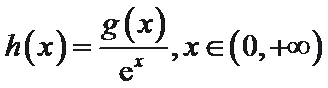
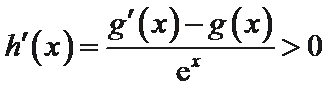
可得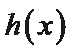
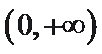
当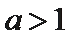
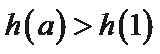
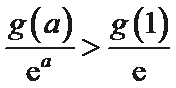
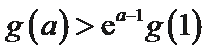
当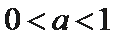
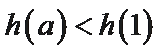
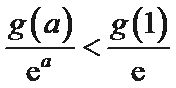
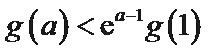
当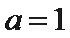
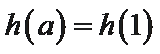
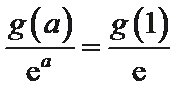
②因为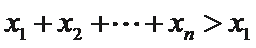
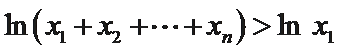
由①可知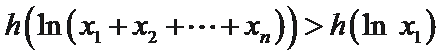

整理得
同理可得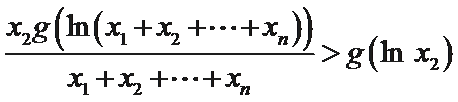
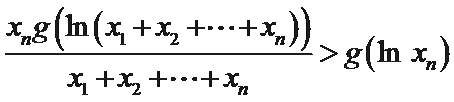
把上面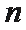
可得
解析
解析已在路上飞奔,马上就到!
知识点
函数性质的综合应用导数的运算数列与函数的综合数列与不等式的综合不等式的性质
1
题型:
单选题
|
18.若



①

②

③


④函数


则以上各命题中正确的个数是 ( )
正确答案
C
解析
解析已在路上飞奔,马上就到!
知识点
命题的真假判断与应用函数性质的综合应用
下一知识点 : 函数的值
扫码查看完整答案与解析