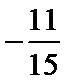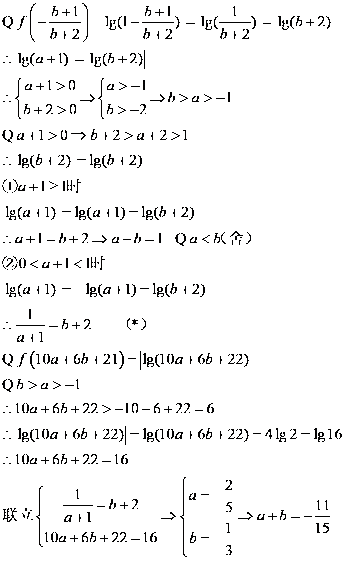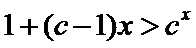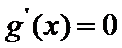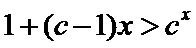- 函数性质的综合应用
- 共80题
设函数
25.讨论函数

26.记


27.在(Ⅱ)中,取


正确答案
(Ⅰ)极小值为
解析
(Ⅰ)



因为

①当

②当

③当







因此,




考查方向
解题思路
(Ⅰ)将



求导得





















易错点
函数求导错误,分类讨论能力弱,计算能力弱
正确答案
解析
:
(Ⅱ)

当

当

由此可知,函数


考查方向
解题思路
当




易错点
绝对值不等式性质运用错误,计算错误,不会合理放缩不等式
正确答案
(Ⅲ)1.
解析
(Ⅲ)



取


由此可知,

考查方向
解题思路
(Ⅲ)当








易错点
平均值不等式的性质,计算能力弱
5. 已知点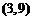
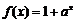

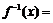
正确答案
解析
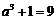
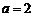
∴
∴
知识点
7. 方程

正确答案
解析

∴
∴
∴
知识点
已知函数
25.若函数


26.令





27.当
正确答案
见解析
解析
考查方向
解题思路
第1问利用导数求函数的单调区间,第2问利用分类讨论思想,讨论参数的值。第3问通过构造函数证明不等式。
易错点
求导数错误,参数的取值范围分类错误
正确答案
见解析
解析
考查方向
解题思路
第1问利用导数求函数的单调区间,第2问利用分类讨论思想,讨论参数的值。第3问通过构造函数证明不等式。
易错点
求导数错误,参数的取值范围分类错误
正确答案
见解析
解析
考查方向
解题思路
第1问利用导数求函数的单调区间,第2问利用分类讨论思想,讨论参数的值。第3问通过构造函数证明不等式。
易错点
求导数错误,参数的取值范围分类错误
设函数
27.若

28.若

29.设

注:
正确答案
见解析
解析
考查方向
解题思路
借助导函数的正负直接求出单调区间
易错点
本题易错在第二问中的信息转化:函数

正确答案
见解析
解析
考查方向
解题思路
根据





易错点
本题易错在第二问中的信息转化:函数

正确答案
见解析
解析
考查方向
解题思路
本题解题思路
借助第二问的结论
易错点
本题易错在第二问中的信息转化:函数

设函数





24.求




25.设



正确答案
(Ⅰ)




又由基本不等式,有
解析
(Ⅰ)由



联立①②解得

当



又由基本不等式,有

考查方向
解题思路
(Ⅰ)将等式










易错点
导函数计算出错。
正确答案
(Ⅱ)由(Ⅰ)得


当




















解析
(Ⅱ)由(Ⅰ)得 

当




设函数 
当













考查方向
解题思路
(Ⅱ)由(Ⅰ)得






易错点
计算量大。
12.已知函数



正确答案
解析




因为





考查方向
解题思路
利用函数的性质将不等式恒成立转换成其他等价形式,由
易错点
求导错误,讨论参数取值范围时考虑不全面
知识点
14.若存在两个正实数x、y,使得等式x+a(y-2ex)(lny-lnx)=0成立,其中e为自然对数的底数,则实数a的取值范围为 .
正确答案
a<0或a≥
解析
∵x+a(y-2ex)(lny-lnx)=0成立
∴
设
即
设

即当t=e时,函数g(t)取得极小值,为g(e)=(e-2e)lne=-e,即g(t)≥g(e)=-e,
若
∴a<0或a≥
考查方向
解题思路
根据函数与方程的关系将方程进行转化,利用换元法转化为方程有解,构造函数求函
数的导数,利用函数极值和单调性的关系进行求解即可.
易错点
能成立问题要转化有解问题,同时要构造函数求最值,同时计算容易出现错误
知识点
15.已知函数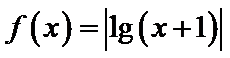
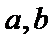
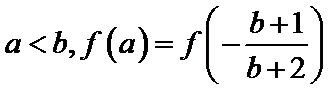
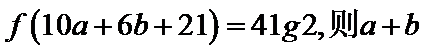
正确答案
考查方向
解题思路
该题解题思路
易错点
主要易错于函数中的绝对值不能去掉,不能判别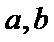
知识点
设函数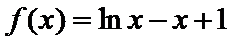
25.讨论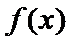
26.证明当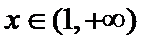
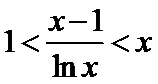
27.设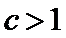
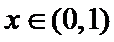
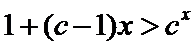
正确答案
(Ⅰ)当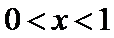
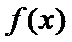
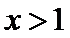
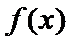
解析
(I)由题设,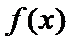
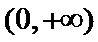
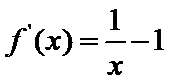
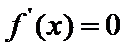
当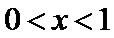
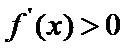
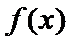
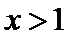
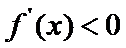
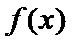
考查方向
解题思路
(I)首先求出导函数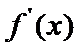
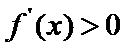
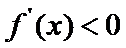
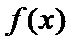
易错点
对利用导数研究函数的单调性和不等式的证明与解法理解出现错误、计算错误
正确答案
(Ⅱ)(II)由(I)知,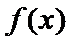
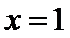
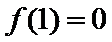
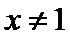
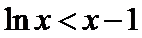
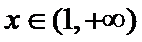
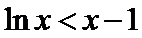
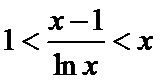
解析
(II)由(I)知,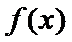
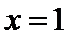
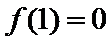
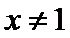
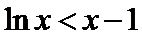
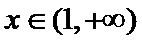
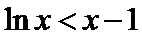
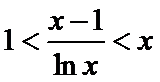
考查方向
解题思路
(II)左端等式可利用(I)的结论证明,右端将左端的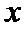

易错点
对利用导数研究函数的单调性和不等式的证明与解法理解出现错误、计算错误
正确答案
(Ⅲ)(III)由题设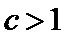
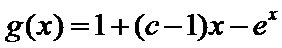
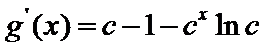
解得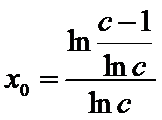
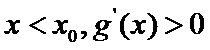
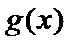
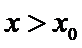
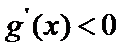
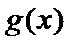
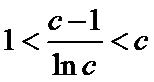
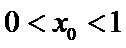
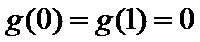
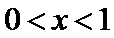
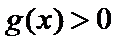
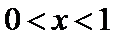
解析
(III)由题设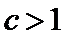
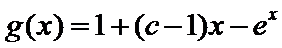
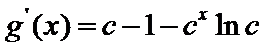
解得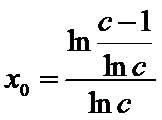
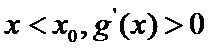
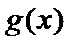
考查方向
解题思路
变形所证不等式构造新函数,然后通过利用导数研究函数的单调性来处理
易错点
对利用导数研究函数的单调性和不等式的证明与解法理解出现错误、计算错误
扫码查看完整答案与解析