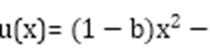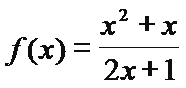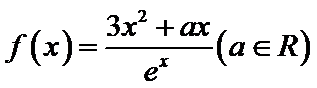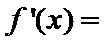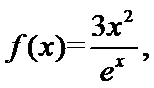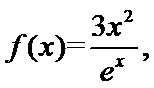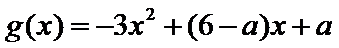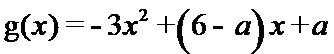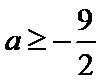- 函数性质的综合应用
- 共80题
已知函数


25.如果函数



26.令


正确答案
(1)

当



当



解析
(Ⅰ)

令




所以



当




当



考查方向
解题思路
先求导后得到原函数的极值点后结合二次函数即可求得a的值,后面利用常用的方法求单调区间;
易错点
不理解函数

正确答案
(2)当


当

解析
(Ⅱ)
令







即函数





若





若










若

此时



若

当



故

若




又

所以

综上,当


当

考查方向
解题思路
按照判别式分类讨论各种情况下零点的个数。
易错点
不会确定分类的标准。
8.已知函数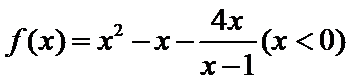
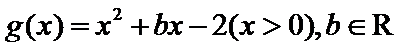
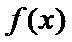
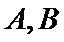
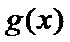
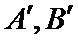
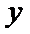
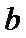
正确答案
解析
设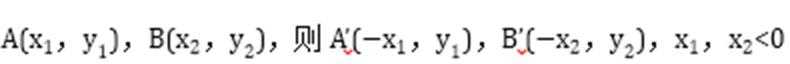

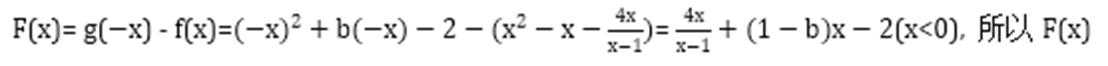
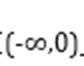
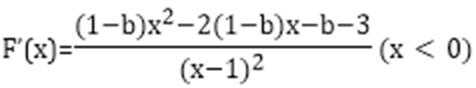
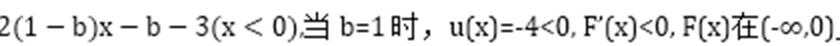
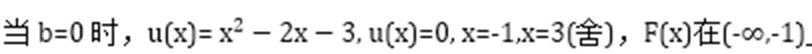
考查方向
解题思路
先设点,后转化方程,得到一个方程有两个负根的问题,然后再构造一个新函数,运用导数来判断函数的有关零点问题
易错点
不能正确理解题目中的对称问题,进而在问题转化过程中进行不下去,对不同情况进行分类讨论不全
知识点
8.设函数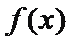
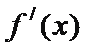

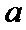



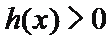

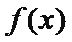
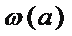
①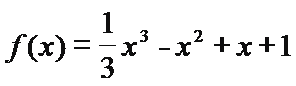
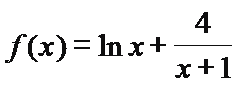
③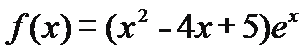
其中具有性质
正确答案
解析
①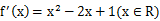
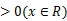
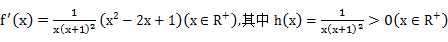
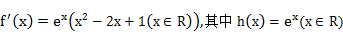
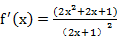
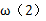
考查方向
解题思路
分别对函数求导,变形与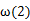
易错点
不理解函数新信息的性质而出错
知识点
已知函数


27.求函数
28.当

29.若


正确答案
见解析
解析



考查方向
解题思路
先根据导数的性质求切线的斜率,进而求出参数的值,得到函数的解析式,利用导数的性质作出函数大致图像,结合图像,利用分类讨论思想求K的取值范围.
易错点
求导错误,函数性质理解错误;分类讨论有重有漏
正确答案
见解析
解析
令

当





∴
考查方向
解题思路
先根据导数的性质求切线的斜率,进而求出参数的值,得到函数的解析式,利用导数的性质作出函数大致图像,结合图像,利用分类讨论思想求K的取值范围.
易错点
求导错误,函数性质理解错误;分类讨论有重有漏
正确答案
见解析
解析




令













考查方向
解题思路
先根据导数的性质求切线的斜率,进而求出参数的值,得到函数的解析式,利用导数的性质作出函数大致图像,结合图像,利用分类讨论思想求K的取值范围.
易错点
求导错误,函数性质理解错误;分类讨论有重有漏
对于函数





已知函数
18.

若区间

正确答案
解析
解:(Ⅱ)
因为区间

考查方向
考察函数的新信息题,具体涉及到函数的定义域,值域,图像等性质
解题思路
先确定函数的值域,利用“可等域函数”, 结合函数的图象,可得函数 
易错点
对新信息理解到位易出错,对函数的综合性质应用不熟练易出现,分类与解题逻辑上的错误,数形结合应用易出错
正确答案
解析
考查方向
考察函数的新信息题,具体涉及到函数的定义域,值域,图像等性质
解题思路
利用“可等域区间”的定义,得出a>0,结合图象,利用区间与对称轴的关系及函数的单调性求出a,b
易错点
对新信息理解到位易出错,对函数的综合性质应用不熟练易出现,分类与解题逻辑上的错误,数形结合应用易出错
(本小题满分12分,(1)小问7分,(2)小问5分)
设函数
23.若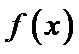
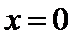
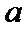
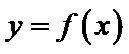
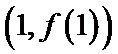
24.若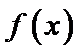
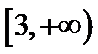
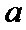
正确答案
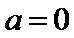
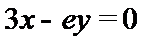
解析
试题分析:本题考查求复合函数的导数,导数与函数的关系,由求导法则可得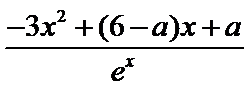
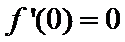
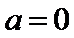
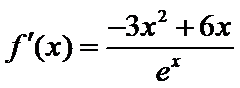
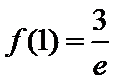
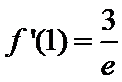
试题解析:(1)对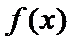
因为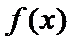
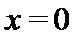
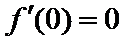
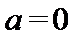
当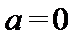
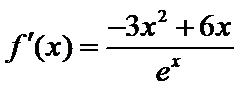
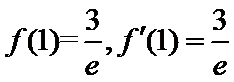
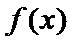
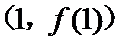
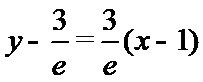
考查方向
解题思路
导数及其应用通常围绕四个点进行命题.第一个点是围绕导数的几何意义展开,设计求曲线的切线方程,根据切线方程求参数值等问题,这类试题在考查导数的几何意义的同时也考查导数的运算、函数等知识,试题的难度不大;第二个点是围绕利用导数研究函数的单调性、极值(最值)展开,设计求函数的单调区间、极值、最值,已知单调区间求参数或者参数范围等问题,在考查导数研究函数性质的同时考查分类与整合思想、化归与转化思想等数学思想方法.
易错点
极值的几何意义.
正确答案
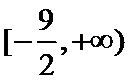
解析
试题分析:(2)由题意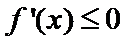
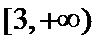
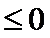
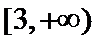
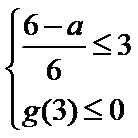
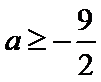
试题解析:(2)由(1)得,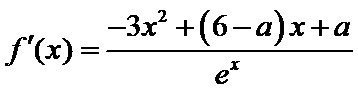
令
由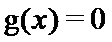
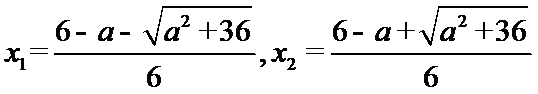
当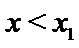
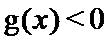
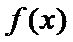
当
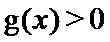
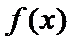
当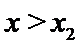
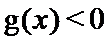
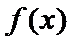
由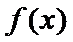
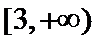
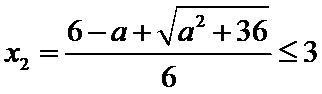
故a的取值范围为
考查方向
解题思路
导数及其应用通常围绕四个点进行命题.第三个点是围绕导数研究不等式、方程展开,涉及不等式的证明、不等式的恒成立、讨论方程根等问题,主要考查通过转化使用导数研究函数性质并把函数性质用来分析不等式和方程等问题的能力,该点和第二个点一般是解答题中的两个设问,考查的核心是导数研究函数性质的方法和函数性质的应用;第四个点是围数性质并把函数性质用来分析不等式和方程等问题的能力,该点和第二个点一般是解答题中的两个设问,考查的核心是导数研究函数性质的方法和函数性质的应用;
易错点
本题涉及第一个点和第二个点,主要注意问题的转化,转化为不等式恒成立,转化为二次函数的性质.
15.已知函数





现有如下命题:
(1)对于任意不相等的实数

(2)对于任意的a及任意不相等的实数

(3)对于任意的a,存在不相等的实数

(4)对于任意的a,存在不相等的实数

其中的真命
正确答案
①④
解析
对于①,因为f '(x)=2xln2>0恒成立,故①正确;
对于②,取a=-8,即g'(x)=2x-8,当x1,x2<4时n<0,②错误;
对于③,令f '(x)=g'(x),即2xln2=2x+a,记h(x)=2xln2-2x,则h'(x)=2x(ln2)2-2,存在












考查方向
解题思路
逐个判断各个选项的正误即可。
易错点
1.不明白题中给出的条件是什么;
对于③④,不知道该如何判断正误。
知识点
已知函数
26.若函数

27.若函数

28.若



注:题目中e=2.71828…是自然对数的底数.
正确答案
(Ⅰ)
解析
试题分析:本题属于函数与导数的基本问题,题目的难度是逐渐由易到难,(1)按照解题步骤求解,(2)要注意转化思想的应用;
(Ⅰ)



又



则切线l的方程又可表示为
由

考查方向
解题思路
本题考查导数的几何意义和导数的应用,解题步骤如下:
1)求导,利用导数的几何意义求出两曲线的切线方程,利用切线相同进行求解;
2)作差,将问题转化为不等式恒成立问题;
3)构造函数,利用导数研究函数的单调性和最值;
4)利用前一步的结论合理赋值进行求解。
易错点
1)不能正确求导;
2)不能合理转化或赋值.
正确答案
(Ⅱ)
解析
试题分析:本题属于函数与导数的基本问题,题目的难度是逐渐由易到难,(1)按照解题步骤求解,(2)要注意转化思想的应用;
a=
(Ⅱ)由题

令



则当x>0时,
由


考查方向
解题思路
本题考查导数的几何意义和导数的应用,解题步骤如下:
1)求导,利用导数的几何意义求出两曲线的切线方程,利用切线相同进行求解;
2)作差,将问题转化为不等式恒成立问题;
3)构造函数,利用导数研究函数的单调性和最值;
4)利用前一步的结论合理赋值进行求解。
易错点
1)不能正确求导;
2)不能合理转化或赋值.
正确答案
(Ⅲ)

解析
试题分析:本题属于函数与导数的基本问题,题目的难度是逐渐由易到难,(1)按照解题步骤求解,(2)要注意转化思想的应用;
(Ⅲ)

由题


当


因为


所以
同理
①+②得
因为
由


所以

所以

考查方向
解题思路
本题考查导数的几何意义和导数的应用,解题步骤如下:
1)求导,利用导数的几何意义求出两曲线的切线方程,利用切线相同进行求解;
2)作差,将问题转化为不等式恒成立问题;
3)构造函数,利用导数研究函数的单调性和最值;
4)利用前一步的结论合理赋值进行求解。
易错点
1)不能正确求导;
2)不能合理转化或赋值.
21.已知函数
(I)若函数


(II)证明:
(III)若不等式

正确答案
见解析
解析
考查方向
解题思路
本题解题思路
1)根据共同的切线的理解得到该点处导函数值与函数值都相等得到t
2)利用单调性确定绝对值内的正负,去掉绝对值号,利用
3)构造关于m的一次函数,把x当作参数消掉m后再使用恒成立问题的解答得出结果
易错点
本题易错在以下几个方面
1)对共同的切线理解不足,第一问出错
2)不能有效去掉绝对值,使用错的解题思想
3)变量间关系不能有效理清
知识点
11.已知函数


①当
②函数
③
④
其中正确命题个数是( )
正确答案
解析
因为f(x)为R上的奇函数,设x>0,-x<0,则



当


同理判断4正确,所以选B
考查方向
解题思路
根据函数的相关性质,结合子题目,依次判断
易错点
求导错误;
知识点
扫码查看完整答案与解析