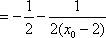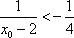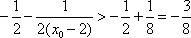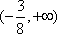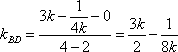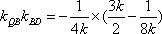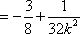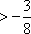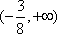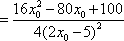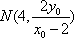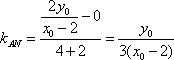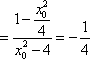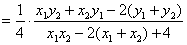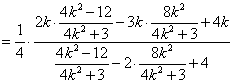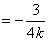- 直线的倾斜角与斜率
- 共278题
若


正确答案
45°或
解析
略
知识点
已知点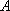
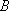

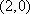
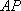
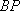


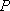
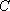
(1)求曲线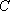
(2)设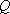
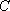
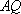
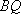
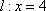
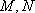
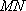
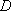

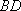
(3)在(2)的条件下,记直线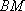
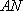
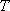

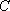
正确答案
见解析。
解析
(1)设动点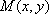
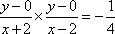

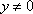
所以曲线
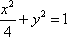
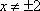
(2)法一:设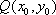

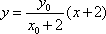
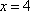
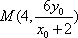
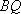
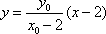
令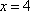
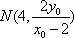
∵ 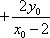
∴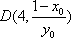
故
∵ 

∴,
∴
∴直线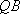

法二:设直线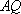
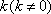
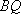
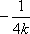
所以直线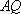
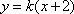
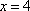
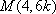
直线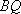
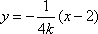
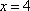
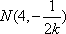
∴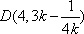
∴
故
∴直线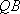
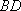
(3)法一:由(2)得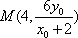
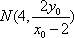
则直线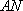
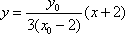
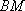
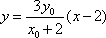
由

∴
∴ 点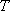

法二:由(2)得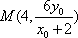
∴ 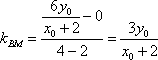
∴
∴ 点
法三:由(2)得,
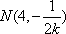
∴ 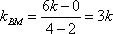
∴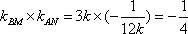


知识点
已知点






(1)求曲线
(2)斜率为








(3)试问:是否存在一个定圆


正确答案
见解析
解析
(1)由题知,有
化简,得曲线

(2)∵直线


∴可设直线

联立方程组

又交点为
∴
∴
(3)答:一定存在满足题意的定圆
理由:∵动圆

∴两圆的圆心之间距离
又



记曲线


∴若定圆的圆心


∴定圆

知识点
在数1和100之间插入




(1)求数列
(2)设



正确答案
见解析
解析
本题考查等比和等差数列,对数和指数的运算,两角差的正切公式等基本知识,考查灵活运用基本知识解决问题的能力,创新思维能力和运算求解能力。
(1)设



①×②并利用
(2)由题意和(1)中计算结果,知
另一方面,利用
得
所以
知识点
已知椭圆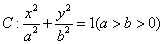
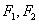
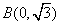
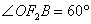
(1)求椭圆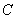
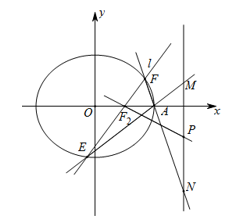
(2)如图,过右焦点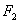
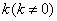
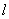
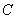
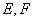
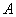
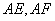
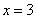
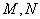
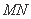
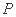
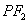
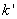
求证: 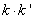
正确答案
见解析
解析
(1)由条件可知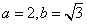
故所求椭圆方程为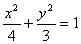
(2)设过点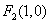
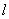
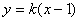
由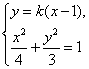
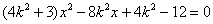
因为点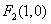
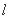
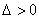
设点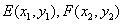
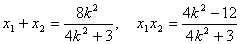
因为直线
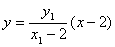
直线
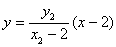
令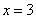
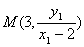
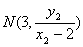
所以点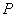
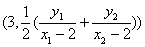
直线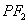
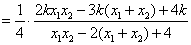
所以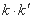
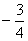
知识点
扫码查看完整答案与解析