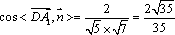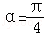- 直线的倾斜角与斜率
- 共278题
1
题型:简答题
|
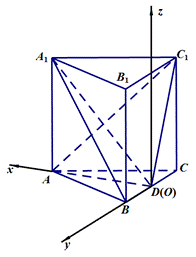
如图,直三棱柱ABC—A1B1C1中,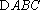
(1)求证:A1B//平面ADC1;
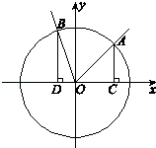
(2)若AB=BB1=2,求A1D与平面AC1D所成角的正弦值。
正确答案
见解析
解析
(1)因为三棱柱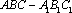
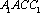
连结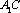
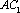
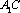
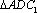
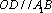
因为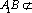
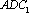
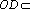
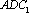
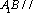
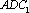
(2)因为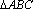
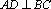
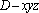
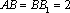
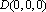
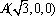
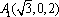
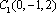
则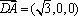
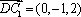
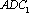
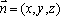
由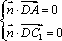
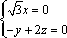
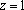
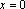
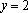
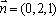
又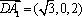
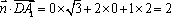
所以
设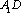
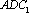

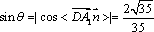
所以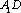
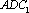
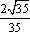
知识点
直线的倾斜角与斜率
1
题型:填空题
|
直线

正确答案
解析
略
知识点
直线的倾斜角与斜率
1
题型:填空题
|
在△


正确答案
解析
略
知识点
直线的倾斜角与斜率
1
题型:简答题
|
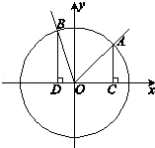
如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且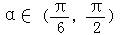
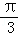
(1)若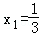
(2)分别过A,B作x轴的垂线,垂足依次为C,D,记△AOC的面积为S1,△BOD的面积为S2,若S1=2S2,求角α的值。
正确答案
(1)
(2)
解析
(1)解:由三角函数定义,得 x1=cosα,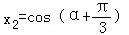
因为 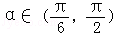
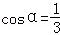
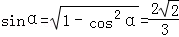
所以 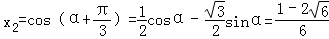
(2)解:依题意得 y1=sinα,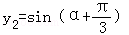
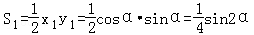

依题意S1=2S2 得 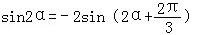


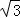
整理得 cos2α=0。
因为 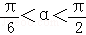
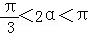
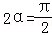
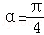
知识点
直线的倾斜角与斜率
1
题型:填空题
|
若圆





正确答案

解析
略
知识点
直线的倾斜角与斜率
下一知识点 : 三点共线
扫码查看完整答案与解析