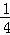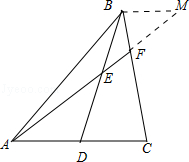直线的倾斜角与斜率
共278题

· 直线的倾斜角与斜率

直线的倾斜角与斜率
共278题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

如图，△中，，，，在三角形内挖去一个半圆（圆心在边上，半圆与、分别相切于点、，与交于点），将△绕直线旋转一周得到一个旋转体。

（1）求该几何体中间一个空心球的表面积的大小；

（2）求图中阴影部分绕直线旋转一周所得旋转体的体积。

正确答案

（1）（2）

解析

（1）连接，则，

设，则，

在中，，

所以，--------------------------（4分）

所以。-----------------（6分）

（2）中，，,，

，-------------------------------（8分）

。

知识点

直线的倾斜角与斜率

题型：填空题

填空题 · 5 分

如图，直线与圆相切于点，割线经过圆心，弦⊥于点，，，则，

正确答案

解析

略

知识点

直线的倾斜角与斜率

题型：填空题

填空题 · 5 分

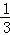
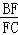
在△ BC中，D是边AC的中点，点E在线段BD上，且满足BE=BD，延长AE交 BC于点F，则的值为　　。

正确答案

解析

如图所示，

过点B作BM∥AC交BF的延长线于点M。

则=，∴==。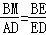

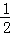
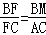
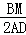
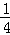
故答案为。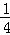

知识点

直线的倾斜角与斜率

题型：填空题

填空题 · 4 分

直线的倾斜角的大小是____________。

正确答案

解析

略

知识点

直线的倾斜角与斜率

题型：简答题

简答题 · 12 分

如图甲，设正方形的边长为,点分别在上,并且满足,如图乙,将直角梯形沿折到的位置,使点在平面上的射影恰好在上。

（1）证明：平面；

（2）求平面与平面所成二面角的余弦值。

正确答案

见解析。

解析

（1）证明：在图甲中，易知,从而在图乙中有，

因为平面，平面，所以平面

（2）解法1、

如图,在图乙中作，垂足为，连接，

由于平面，则，

所以平面，则，

所以平面与平面所成二面角的平面角，

图甲中有，又，则三点共线，

设的中点为，则，易证，所以，，

又由，得，

于是，，

在中，，即所求二面角的余弦值为

解法2、

如图,在图乙中作，垂足为，连接，由于平面，则，所以平面，则，图甲中有，又，则三点共线，

设的中点为，则，易证，所以，则；

又由，得，

于是，，

在中，

作交于点，则，以点为原点，分别以所在直线为轴，建立如图丙所示的空间直角坐标系，则、、、，则（坐标系、坐标、向量各1分） ……11分

显然，是平面的一个法向量，

设是平面的一个法向量，则，即，不妨取，则，

设平面与平面所成二面角为，可以看出，为锐角，所以，，所以，平面与平面所成二面角的余弦值为。

知识点

直线的倾斜角与斜率

继续学习学习下一知识点

下一知识点 : 三点共线

百度题库 > 高考 > 理科数学 > 直线的倾斜角与斜率

扫码查看完整答案与解析