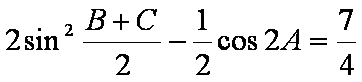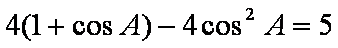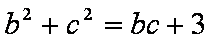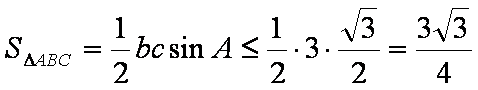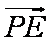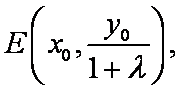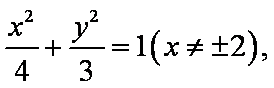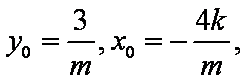- 直线的倾斜角与斜率
- 共278题
如图,直线








(1)求证:直线

(2)若



正确答案
见解析
解析
解析: (1)如图,连接


(2)
又







设

知识点
如图,四棱锥P-ABCD的底面ABCD为直角梯形,其中


(1)求证:BE∥平面PAD;
(2)若



正确答案
见解析。
解析
设AB=a,PA=b,如图建立空间坐标系,则A(0,0,0),B(a, 0, 0), P(0, 0, b)
C(2a,2a,0),D(0,2a,0),E(a,a,b/2)…………2分
(1)
∴
∵

(2)∵BE⊥平面PCD∴BE⊥PC即
又∵

设平面BDE的一个法向量为n1=(x,y,z),又
∴
∵AP⊥面BCD∴平面BDC的一个法向量为n2=(0,0,1)…………10分
∴cos<n1,n2>=
∴平面BDE与平面BDC夹角的余弦值为
知识点
在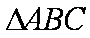
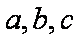
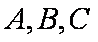
(1)求角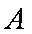
(2)若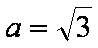
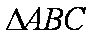
正确答案
见解析
解析
(1)由2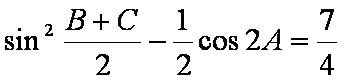
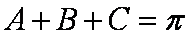
2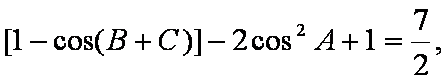
即
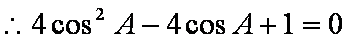
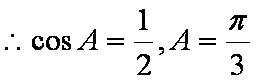
(2)由余弦定理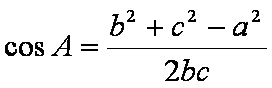
又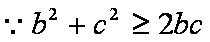
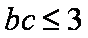
所以
所以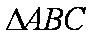
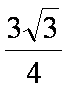
知识点
已知四边形







(1)求证:直线

(2)在线段




正确答案
见解析
解析
解:(1) 如图建立空间直角坐标系
则
设平面
则
令

又
而
所以 

所以

(2) 假设在线段


设

则
则
若平面

即
得:
所以,存在点



知识点
已知点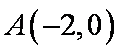
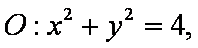
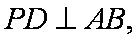
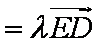
(1)求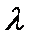
(2)若点Q、R是曲线E上不同的的点,且PQ、PR与曲线E相切,求△OQR面积的最小值。
正确答案
见解析。
解析
(1)易得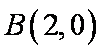
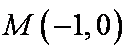
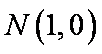
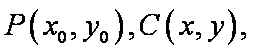
直线PA与BE交于C,
故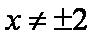
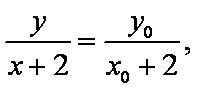
且
①②相乘得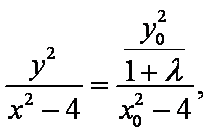
即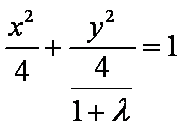
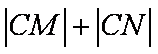
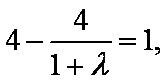
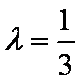
即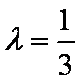
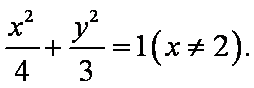
(2)设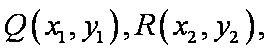
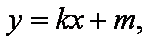
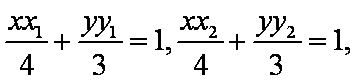
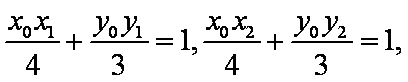
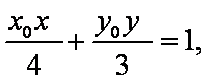
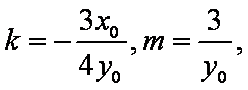
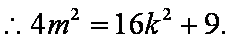
另一方面,由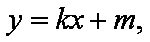
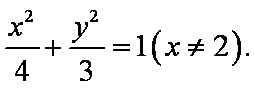
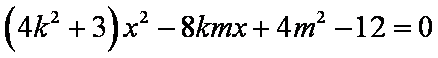
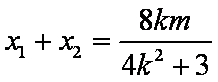
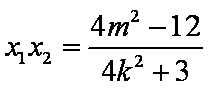
所以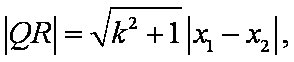
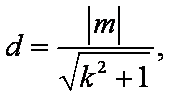
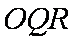
将③④⑤代入消去k,得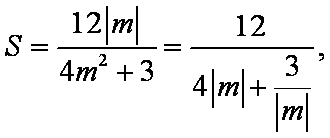
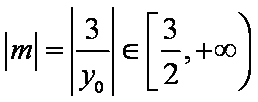
易知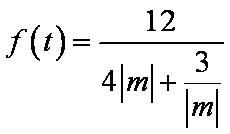
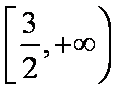
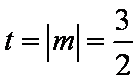

知识点
扫码查看完整答案与解析