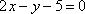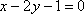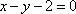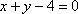- 直线的倾斜角与斜率
- 共278题
圆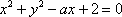
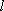
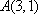
正确答案
解析
略
知识点
如图,三棱柱









(1)求证:

(2)在棱




正确答案
见解析。
解析
(1)证明:
取


又

在三棱柱








(2)设

部分的体积之比为1︰15,
则



所以符合要求的点
知识点
若直线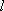
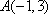
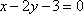
正确答案
解析
略
知识点
在极坐标系中,直线

正确答案
解析
略
知识点
在△ABC中角A.B.C的对边分别为
(1)若

(2)若


正确答案
见解析。
解析
因为
所以
由正弦定理,得
即
又


(1)



得

(2)若

由正弦定理,得
设


所以
即


知识点
如图,正方形







(1)当点



(2)当平面



正确答案
见解析。
解析
(1)以直线









∴
又,

∵
∴

(2)设

设


设


取

又由题设,

∴
即点




∴ 
知识点
已知直线




正确答案
解析
略
知识点
选修4-1:几何证明选讲
如图,圆O1与圆O2相交于A.B两点,AB是圆O2的直径,过A点作圆O1的切线交圆O2于点E,并与BO1的延长线交于点P,PB分别与圆O1.圆O2交于C,D两点。
求证:(1)PA·PD=PE·PC;
(2)AD=AE。
正确答案
见解析。
解析
(1)


又


由①,②得
(2)连结



∵

∴
∴

由(1)知





又∵

又
∴
知识点
已知三棱柱ABC—A1B1C1,A1在底面ABC上的射影恰为AC的中点O,∠BCA=90°,AC=BC=2,又知BA1⊥AC1。
(1)求证AC1⊥平面A1BC;
(2)求锐二面角A—A1B—C的余弦值。
正确答案
见解析。
解析
方法1:(1)证明:由∠BCA=90°,得BC⊥AC
因为A1O⊥底面ABC,所以A1O⊥BC …………2分
因为A1O∩AC=O,所以BC⊥平面A1AC,所以BC⊥AC1, …………4分
因为BA1⊥AC1,BA1∩BC=B,所以AC1⊥平面A1BC……………………6分
(2)设AC1∩A1C =Q,作QE⊥A1B于E,连接AE, 由(Ⅰ)知A1B⊥AE,
所以∠AEQ为二面角A-A1B-C的平面角
在Rt△A1BC中,QE=

所以
∴二面角A-A1B-C的余弦值为
方法2;如图,取AB的中点E,则OE//BC,
因为BC⊥AC,所以OE⊥AC
又A1O⊥平面ABC,以OE⊥OC,
OA1为x,y,z轴建立空间直角坐标系,则A(0,-1,0)。
C(0,1,0),B(2,1,0),A1(0,0,t),C1(0,2,t),t>0.………2分
(1)


∵
∴AG⊥CB,
又BA1⊥AC1,从而AC1⊥平面A1BC,…………6分
(2)∵


解得:
由(1)知平面A1BC的一个法向量

设平面A1AB 的法向量为n=(x,y,z),



…………10分
故cos<
∴锐二面角A—A1B—C的余弦值为
知识点
若点P在直线




正确答案
解析
画出图形,由题意l2与圆C只一个交点,说明







知识点
扫码查看完整答案与解析