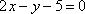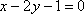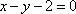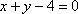直线的倾斜角与斜率
共278题

· 直线的倾斜角与斜率

直线的倾斜角与斜率
共278题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

圆与直线相切于点，则直线的方程为( )

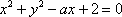
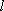
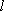
正确答案

解析

略

知识点

直线的倾斜角与斜率

题型：简答题

简答题 · 14 分

如图，三棱柱中，平面,、分别为、的中点，点在棱上，且.

（1）求证：平面;

（2）在棱上是否存在一个点，使得平面将三棱柱分割成的两部分体积之比为115，若存在，指出点的位置；若不存在，说明理由.

正确答案

见解析。

解析

（1）证明：

取的中点M，为的中点，

又为的中点，

在三棱柱中，分别为的中点，

为平行四边形，

平面，平面

平面

（2）设上存在一点,使得平面EFG将三棱柱分割成两

部分的体积之比为1︰15，

则

，，

所以符合要求的点不存在

知识点

直线的倾斜角与斜率

题型：简答题

简答题 · 12 分

在△ABC中角A.B.C的对边分别为设向量

（1）若=，求A；

（2）若的外接圆半径为1，且试确定的取值范围。

正确答案

见解析。

解析

因为

所以，-------------------------------------------1分

由正弦定理，得，

即-------------------------------------------------2分

又所以即

，--------------------------------3分

（1）= ------4分

，

得， 6分

（2）若则，

由正弦定理，得 8分

设=，则，

所以-------------------------------------------10分

即，所以实数的取值范围为，---------12分

知识点

直线的倾斜角与斜率

题型：填空题

填空题 · 5 分

已知直线与圆相交于两点，且则的值是

正确答案

解析

略

知识点

直线的倾斜角与斜率

题型：简答题

简答题 · 12 分

选修4-1：几何证明选讲

如图，圆O1与圆O2相交于A.B两点，AB是圆O2的直径，过A点作圆O1的切线交圆O2于点E，并与BO1的延长线交于点P，PB分别与圆O1.圆O2交于C，D两点。

求证：（1）PA·PD=PE·PC；

（2）AD=AE。

正确答案

见解析。

解析

（1）分别是⊙的割线∴ ①（2分）

又分别是⊙的切线和割线∴ ② （4分）

由①，②得（5分）

（2）连结.，设与相交于点

∵是⊙的直径

∴

∴是⊙的切线，（6分）

由（1）知，∴∥∴⊥, （8分）

又∵是⊙的切线，∴

又，∴

∴ （10分）

知识点

直线的倾斜角与斜率

继续学习学习下一知识点

下一知识点 : 三点共线

百度题库 > 高考 > 理科数学 > 直线的倾斜角与斜率

扫码查看完整答案与解析