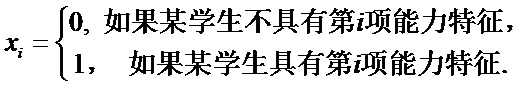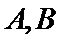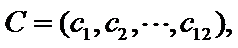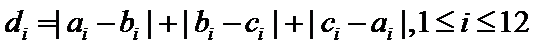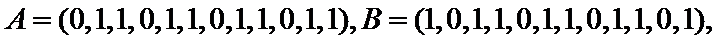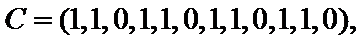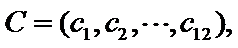排列与组合的综合
共7题

· 排列与组合的综合

排列与组合的综合
共7题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

用数字1，2，3，4，5组成没有重复数字的五位数，其中奇数的个数为

A24

B48

C60

D72

正确答案

知识点

排列、组合及简单计数问题排列与组合的综合

题型：简答题

简答题 · 10 分

设(1－x)n＝a0＋a1x＋a2x2＋…＋anxn，n∈N*，n≥2．

33.设n＝11，求|a6|＋|a7|＋|a8|＋|a9|＋|a10|＋|a11|的值；

34.设bk＝ak＋1(k∈N，k≤n－1)，Sm＝b0＋b1＋b2＋…＋bm(m∈N，m≤n－1)，求| |的值．

第(1)小题正确答案及相关解析

正确答案

（1）1024；

解析

解：（1）因为ak＝(－1)k ，

当n＝11时，|a6|＋|a7|＋|a8|＋|a9|＋|a10|＋|a11|＝

＝＝1024．

考查方向

本题考查了二项式定理和性质应用，考查化简整理运算能力

解题思路

本题考查二项式定理和性质，解题步骤如下：

（1）由二项式定理可得ak＝(－1)k，再由二项式系数的性质，可得所求和为210；

＝(－1)k－1 －(－1)k ，讨论m=0和1≤m≤n-1时，计算化简即可得到所求值．

易错点

二项式定理和性质不会熟练应用，容易计算错误

第(2)小题正确答案及相关解析

正确答案

（2）1

解析

（2）bk＝＝＝，

当1≤k≤n－1时，bk＝(－1)k＋1 ＝ (－1)k＋1 ＝(－1)k＋1＋(－1)k＋1

＝(－1)k－1－(－1)k ．

当m＝0时，||＝||＝1．

当1≤m≤n－1时，

Sm＝－1＋ [(－1)k－1 ，

所以||＝1．综上，||＝1．

考查方向

本题考查了二项式定理和性质应用，考查化简整理运算能力

解题思路

本题考查二项式定理和性质，解题步骤如下：

（2）由组合数的阶乘公式可得bk＝ (－1)k＋1 ，再由组合数的性质，可得当1≤k≤n－1时，bk

＝(－1)k－1 －(－1)k ，讨论m=0和1≤m≤n-1时，计算化简即可得到所求值．

易错点

二项式定理和性质不会熟练应用，容易计算错误

题型：填空题

填空题 · 5 分

13. 已知正四面体，点、、、、、分别是所在棱的中点，如图. 则当，，且时，数量积的不同数值的个数为 .

正确答案

解析

设正四面体的棱长为2；

（1）当直线直线所在直线平行或重合时，，，

（2）当直线直线所在直线相交时，，，

（3）当直线直线所在直线异面时，，

由以上情况可知，数量积的不同数值的个数为4+4+1=9.

考查方向

本题主要考查空间两条直线的位置关系，向量的数量积等知识，意在考查考生的空间想象能力和分类讨论的能力。

解题思路

1.先将题中给出的向量和所给的向量分类；

2.计算在不同类里数量积的不同值后即可得到答案。

易错点

1.不知如何分类导致结果多或者少；

2.无法理解题中的条件

知识点

空间几何体的结构特征排列与组合的综合

题型：填空题

填空题 · 5 分

14．某班主任在其工作手册中，对该班每个学生用十二项能力特征加以描述．每名学生的第

（）项能力特征用表示，

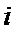
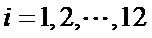
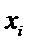
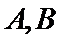
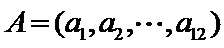
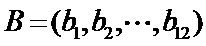
若学生的十二项能力特征分别记为，，则

两名学生的不同能力特征项数为（用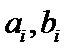表示）．如果两个

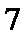
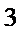
同学不同能力特征项数不少于，那么就说这两个同学的综合能力差异较大．若该班有名学生两两综合能力差异较大，则这名学生两两不同能力特征项数总和的最小值为．

正确答案

； 22。

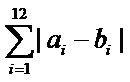
解析

设第三个学生为

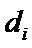
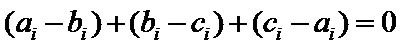
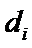
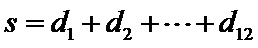
因为的奇偶性和一样，所以为偶数，3名学生两两不同能力特征项数总和为偶数，

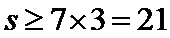
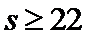
又，所以。

取

则不同能力特征项数总和恰为22 ，所以最小值为22 ．

考查方向

本题主要考查了考生分析问题解决问题的能力，逻辑推理能力及数据处理能力，较难。

解题思路

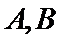
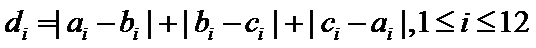
理解清题意即可得到两名学生的不同能力特征项数。理解三个学生时为从而得到结。

易错点

本题不易读懂题意，特别是对“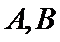两名学生的不同能力特征项数”和“名学生两两不同能力特征项数总和的最小值”的理解不到位而出错。本题易出现逻辑上的混乱，从而导致判断出错。

知识点

排列、组合的实际应用排列与组合的综合

题型：单选题

单选题 · 5 分

阅读下面的程序框图，则输出的=

A14

B20

C30

D55

正确答案

解析

略

知识点

排列与组合的综合

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 理科数学 > 排列与组合的综合

扫码查看完整答案与解析