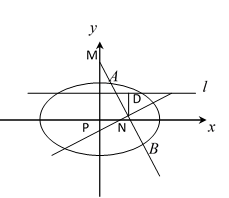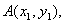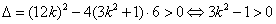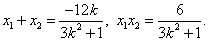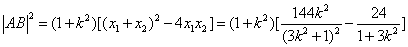- 圆锥曲线的定点、定值问题
- 共43题
已知直线











(1)求椭圆
(2)(ⅰ) 设直线



(ⅱ)求线段
正确答案
见解析
解析
(1).椭圆 

(2)(ⅰ)设点

∴

∵点

∴
(ⅱ) 设直线

则

∵
∴ 直线

∴
故
∴
当且仅当

∴


知识点
如图,已知椭圆C:


(1)求椭圆C的方程;
(2)过点


正确答案
见解析。
解析
(1)∵△AF1F2的周长为
∴

又

∴椭圆C的方程为
(2)由题意知,直线l的斜率必存在,
设其方程为
由
得
则
由
∴

设点R的坐标为(

得
∴
解得
而
∴
故点R在定直线
知识点
已知椭圆


(1)求椭圆
(2)过点















正确答案
见解析
解析
(1)依题得


所以椭圆

(2)根据已知可设直线

由

设

直线


令
则

所以

知识点
已知椭圆







(1)求椭圆
(2)证明直线

正确答案
见解析
解析
(1)由题意知:
所以,焦点坐标为

(2)由题意知:直线PB的斜率存在,设直线PB的方程为



由
则
直线AE的方程为


又


把(1)代入(3)式,整理得


知识点
已知椭圆




(1)求椭圆
(2)已知点







正确答案
见解析
解析
(1)解:由题意知:
根据椭圆的定义得:

所以 
所以 椭圆

(2)证明:当直线

则 
当直线



由

显然

因为 

所以

即 
知识点
抛物线









(1)求抛物线
(2)当圆心

(3)当圆心



正确答案
见解析。
解析
(1)
知识点
已知抛物线

(1)求椭圆标准方程;
(2)设动点







(3)若









正确答案
见解析。
解析
(1)由题设可知:因为抛物线

所以椭圆中的
故
故椭圆的标准方程为:
(2)设
由
由直线OM与ON的斜率之积为

由①②可得:
M、N是椭圆上的点,故
故
由椭圆定义可知存在两个定点
使得动点P到两定点距离和为定值
(3)设

由题设可知

将③代入④可得:

点

故
知识点
已知圆






(1)求椭圆
(2)已知直线












正确答案
(1)
(2)
解析
(1)设椭圆的焦距为



所以


(2)设





由直线



所以


所以
点



则
显然,若点



因为

所以
解得

知识点
设







(1)若

(2)当
(3)在满足(1)的条件下,求证:
正确答案
见解析。
解析
(1)设




同理,
令 



由①,②,得

∴
(2)当

(3)设 

所以
∴P到MN的距离为
∴
∴为定值
知识点
已知椭圆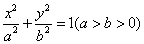
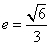
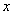
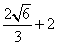
(1)求椭圆的标准方程;
(2)设点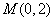
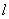
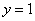
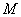
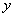
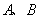
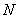
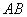
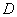
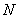
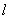
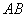
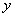
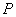
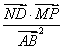
正确答案
见解析。
解析
(1)解:由题意可得
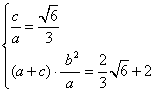
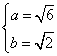
∴椭圆的标准方程为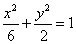
(2)设直线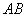
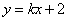
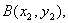
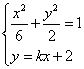
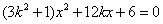
∵直线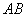
∴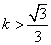
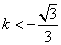
由
得
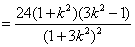
设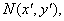
∴直线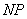
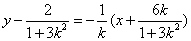
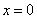
-----------------11分
∴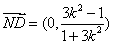
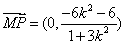
∴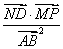
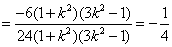
知识点
扫码查看完整答案与解析