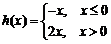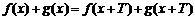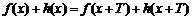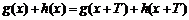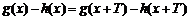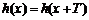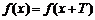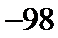函数的周期性
共56题

· 函数的周期性

函数的周期性
共56题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

9.已知函数f(x)的定义域为R.当x<0时，；当时，；当时， .则f(6)=

A−2

B−1

正确答案

知识点

函数的周期性函数性质的综合应用

题型：填空题

填空题 · 5 分

已知函数f（x）是定义在R上的周期为2的奇函数，当0＜x＜1时，f（x）=，则f（）+ f（1）= 。

正确答案

-2

知识点

函数奇偶性的性质函数的周期性函数的值

题型：单选题

单选题 · 5 分

18. 设是定义域为的三个函数，对于命题:①若，，均为增函数，则中至少有一个为增函数；②若，，均是以为周期的函数，则均是以为周期的函数，下列判断正确的是( )

A①和②均为真命题

B①和②均为假命题

C①为真命题，②为假命题

D①为假命题，②为真命题

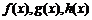
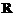
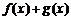
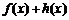
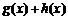
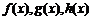
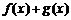
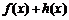
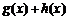
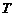
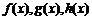
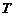
正确答案

解析

①不成立，可举反例

, ,

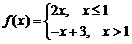
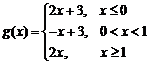
②

前两式作差，可得

结合第三式，可得,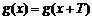

也有

∴②正确

故选D

知识点

复合函数的单调性函数的周期性

题型：填空题

填空题 · 5 分

14.已知函数是周期为的奇函数，当时，，则

．

正确答案

解析

由函数是周期为的奇函数得

，

故

考查方向

本题主要考查函数的奇偶性和周期性以及对数的运算性质等知识，意在考查考生的转化能力和运算求解能力。

解题思路

1.利用函数为周期为的奇函数将化简为；2．利用题中给出的解析式得到。

易错点

1.不会将化简到给定的区间；2.利用对数的运算性质运算时出错。

知识点

抽象函数及其应用函数的周期性函数的值

题型：填空题

填空题 · 18 分

23．已知函数，若存在常数T（T>0），对任意都有，则称函数为T倍周期函数．

（1）判断是否是T倍周期函数，并说明理由；

（2）证明：是T倍周期函数，且T的值是唯一的；

（3）若是2倍周期函数，，，表示的前n项和，，若恒成立，求a的取值范围．

正确答案

（1）不是；

（2）略；

（3）或．

解析

（1）设：

则对任意x恒成立

无解不是T倍周期函数

（2）设：则

对任意x恒成立

下证唯一性：

若，矛盾

是唯一的

（3）

同理：

显然：且

即单调递减

恒成立，

① 时

解得： ② 时

解得：

或

考查方向

本题考查函数性质、数列求和、数列的单调性、恒成立问题，考查了分类讨论的思想，考查学生综合分析问题的能力，既是新定义的学习型题，又是函数与数列相结合的综合题，属于中档题，在近几年各省市高考中出现的频率很高，常以压轴题的形式出现，整合函数、数列、解析几何、三角、向量等知识，体现数学多种思想方法．

解题思路

（1）假设h（x+T）=T•h（x），进而得出结论；

（2）通过设g（x+T）=T•g（x）并令x=0可知，分、两种情况证明唯一性即可；

（3）利用f（n+2）=2•f（n）及f（1）=1、f（2）=-4分别计算出n为奇数、偶数时的值，进而利用等比数列的求和公式计算可知S2n=-3（2n-1）、S2n-1=-2n+3，计算即得，再将恒成立问题转化为的最大值问题，分类讨论求得a的取值范围．

易错点

1．对新定义的概念T倍周期函数的不理解；

2．恒成立问题转化为求最值问题，不知道如何转化；

3．不知道如何求得的最大值．

知识点

抽象函数及其应用函数的周期性函数恒成立问题

题型：单选题

单选题 · 5 分

4．已知在上是奇函数,且满足,当时,，则（）

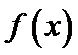
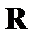
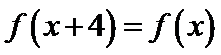
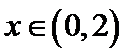
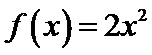
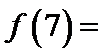
正确答案

解析

f(7)= f(4+3)=f(3)=- f(-3)=- f(4-3)=- f(1)

f(1)可代入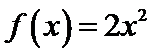中求解

考查方向

本题主要考查函数的周期性与奇偶性。

解题思路

利用周期性以及奇偶性将问题转化到（0，2）区间解决。

易错点

将f(7)转化到f(3)后无从下手

知识点

函数奇偶性的性质函数的周期性函数的值

棒棒哒，已学完当前知识点学习下一知识点

下一知识点 : 函数性质的综合应用

百度题库 > 高考 > 理科数学 > 函数的周期性

扫码查看完整答案与解析