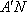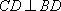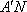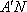- 直线与直线垂直的判定与性质
- 共82题
如图,在直角梯形ABEF中,BE∥AF,∠FAB=90°,CD∥AB,将DCEF沿CD折起,使∠FDA=60°,得到一个空间几何体。
(1)求证:BE∥平面ADF;
(2)求证:AF⊥平面ABCD;
(3)求三棱锥E-BCD的体积。
正确答案
见解析。
解析
(1)
由已知条件可知






同理

又




又

∴

(2)由于






(3)法一:


又


法二:取


由(2)易知





又





知识点
在直角梯形ABCD中,ADBC,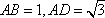
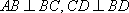
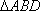
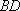
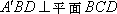
(1)求证: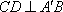
(2)求三棱锥
(3)在线段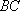
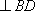
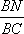
正确答案
见解析。
解析
(1)∵平面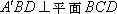
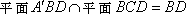
∴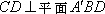
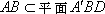
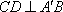
(2)如图(1)在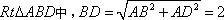
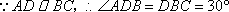
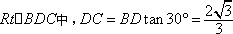
∴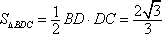
如图(2),在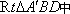
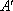

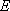
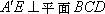
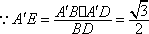
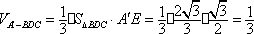
(3)在线段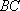
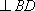
如图(2)在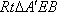
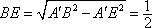
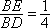
过点E做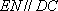
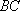
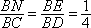
∵
又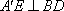
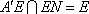
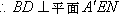
又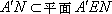
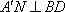
∴在线段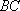
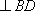
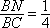
知识点
如图










(1)求证:

(2)求证:

(3)求五面体
正确答案
见解析。
解析
(1)证明:连接






∵

∴


∵





∴

∵
∴


∴四边形
∴


∵



∴

(2)证法1:取



由(1)知,


∴四边形
∴


在Rt△



∴
在△



∴
∴
∴

∵四边形
∴
∵




∴

证法2:在Rt△


∴
在△

∴
∴
∵

∴
∵




∴

∵

∴
∵四边形
∴
∵




∴

(3)
解:连接
在Rt△

∴
由(2)知



∴

∵



∴

∴四棱锥

∴三棱锥

∴五面体

知识点
给定空间中的直线l及平面
正确答案
解析
略
知识点
设m,n是平面


正确答案
解析
略
知识点
扫码查看完整答案与解析