- 函数的值域及其求法
- 共87题
已知函数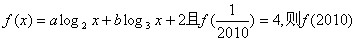
正确答案
解析
略
知识点
某同学为研究函数








正确答案

解析
略
知识点
若
(1)讨论
(2)当



正确答案
见解析。
解析
由
(1))令
则
①当


故
所以
所以

②当


故
所以
所以

③当

又因为

(i)当

当

所以

(ii) 当
令
令
故此时
减区间为
综上得:①当


②当

减区间为
③当


(2)因为在
所以
即
整理得
当
所以
知识点
已知定义在正整数集上的函数
(1)


则
正确答案
2027091
解析
略
知识点
已知函数
(1)若函数

(2)若对于任意的


正确答案
(1)
(2)
解析
(1)
于是,根据题设有
解得

当


当

所以 
(2)法一:


所以


因为 
所以 

所以 

即 
又
所以 当

所以 
所以 

法二:


即


即
令
当


当


又

综上,

知识点
扫码查看完整答案与解析



























