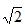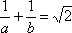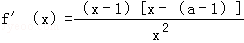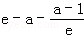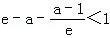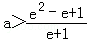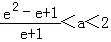- 函数的值域及其求法
- 共87题
已知



正确答案
解析
略
知识点
已知函数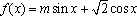
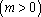
(1)求函数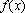
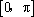
(2)已知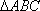
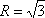
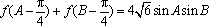
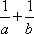
正确答案
(1)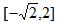
解析
(1)由题意,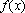
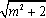
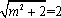
而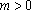
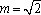
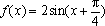
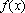
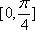
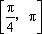
所以函数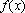
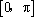
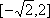
(2)化简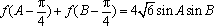
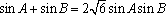
由正弦定理,得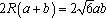
因为△ABC的外接圆半径为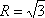
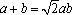
所以
知识点
设


正确答案
解析
略
知识点
在区间[﹣1,2]上随即取一个数x,则x∈[0,1]的概率为
。
正确答案
解析
在数轴上表示区间[0,1]的线段的长度为1;
示区间[﹣1,2]的线段长度为3
故在区间[﹣1,2]上随即取一个数x,则x∈[0,1]的概率P=
故答案为:
知识点
已知a<2,
(1)求f(x)的单调区间;
(2)若存在x1∈[e,e2],使得对任意的x2∈[﹣2,0],f(x1)<g(x2)恒成立,求实数a的取值范围。
正确答案
见解析
解析
解:(1)由题意可得f(x)的定义域为(0,+∞),
∵a<2,∴a﹣1<1
①当a﹣1≤0,即a≤1,∴x∈(0,1)时,f′(x)<0,f(x)是减函数,x∈(1,+∞)时,f′(x)>0,f(x)是增函数;
②当0<a﹣1<1,即1<a<2,∴x∈(0,a﹣1)∪(1,+∞)时,f′(x)>0,f(x)是增函数,x∈(a﹣1,1)时,f′(x)<0,f(x)是减函数;
综上所述,当a≤1时,f(x)的单调减区间是(0,1),单调增区间是(1,+∞);当1<a<2时,f(x)的单调减区间是(a﹣1,1),单调增区间是(0,a﹣1),(1,+∞);
(2)由题意,存在x1∈[e,e2],使得对任意的x2∈[﹣2,0],f(x1)<g(x2)恒成立,等价于对任意x1∈[e,e2]及x2∈[﹣2,0],f(x)min<g(x)min,
由(1),当a<2,x1∈[e,e2]时,f(x)是增函数,f(x)min=f(e)=
∵g′(x)=x(1﹣ex),对任意的x2∈[﹣2,0],g′(x)≤0
∴g(x)是奇函数,∴g(x)min=g(0)=1
∴
∴
∵a<2
∴
知识点
扫码查看完整答案与解析