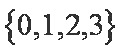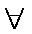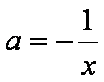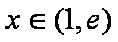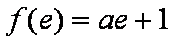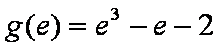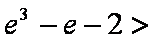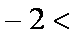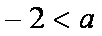- 函数的值域及其求法
- 共87题
已知
(1)求
(2)试问过点

正确答案
见解析。
解析
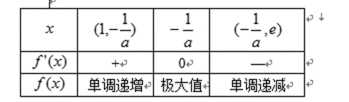
(1)
(ⅰ)当


(ⅱ)当






(2)设切点为


即
令








又





知识点
已知是






正确答案
解析
因为

∴f(x)为增函数且m≠0,
若m>0时,由复合函数的单调性可知f(mx)和mf(x)均为增函数,此时不符合题意。
若m<0时,有
因为



知识点
定义在正实数集上的函数
①存在常数




(1)求证:对于任意正实数

(2)证明:

(3)若不等式

正确答案
见解析。
解析
(1)证明:令
则
所以
(2)证明:设
则必

而
即
所以

(3)令
则
故

所以


知识点
已知函数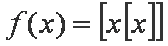
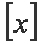
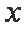
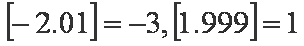
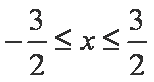
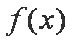
正确答案
解析
略
知识点
在直角坐标系





(1)求
(2)过点











正确答案
见解析
解析
解:(1)





(2)设直线


由

由题意


化简得:
当




知识点
已知函数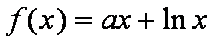
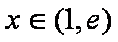
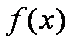
(1)求实数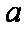
(2)求函数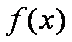
(3)函数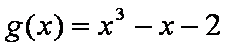
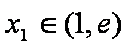
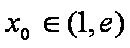
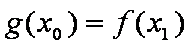
正确答案
见解析
解析
解:(1)由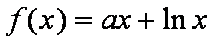
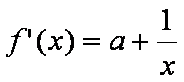
令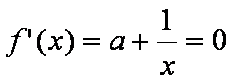
∵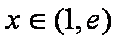
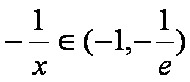
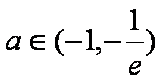
又因为
所以,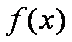
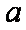

(2)由(1)可知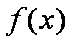
又∵ 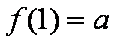
由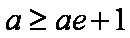
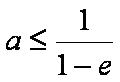
∴当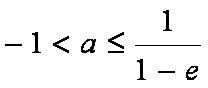
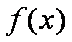
当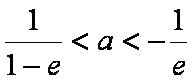
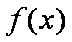
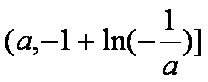
(3)证明:由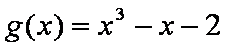
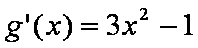
令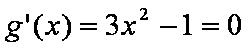
令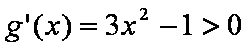
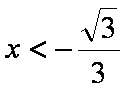
又∵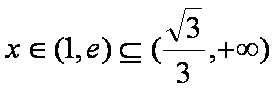
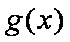
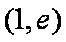
∵ 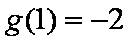
∴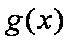
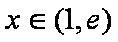
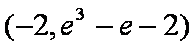
∵ 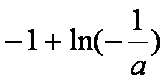
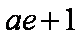
∴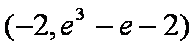
∴ 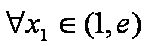
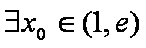
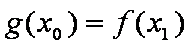
知识点
已知函数
(1)若不等式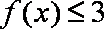
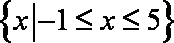
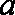
(2)在(1)的条件下,若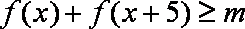
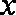
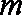
正确答案
(1)a=2(2)
解析
解析:(1)由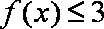
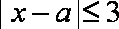
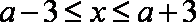
又已知不等式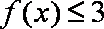
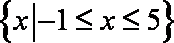

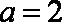
(2)当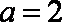

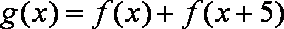
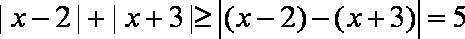
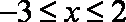
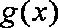
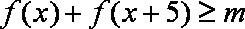
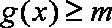
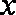
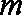
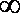
知识点
已ΔABC的内角A,B,C对的边分别为 a,b,c 



(1)求角A的大小;
(2)若a = 1,求b +c的取值范围.
正确答案
(1)
解析
(1)由


再由正弦定理得:
又
所以
又
(2)由正弦定理得


故b+c的取值范围为(1,2] .……12分
知识点
19.已知数列{an}是正数等差数列,其中a1=1,且a2、a4、a6+2成等比数列;数列{bn}的前n项和为Sn,满足2Sn+bn=1.
(1)求数列{an}、{bn}的通项公式;
(2)如果cn=anbn,设数列{cn}的前n项和为Tn,是否存在正整数n,使得Tn>Sn成立,若存在,求出n的最小值,若不存在,说明理由.
正确答案
见解析。
解析
(1)设数列{an}的公差为d,
∵a1=1,且a2、a4、a6+2成等比数列,
∴依条件有
即

所以an=a1+(n﹣1)d=1+(n﹣1)=n.
由2Sn+bn=1,得
当n=1时,2S1+b1=1,解得
当n≥2时,
所以
所以数列{bn}是首项为

故
(2)由(1)知,
所以

得
又
所以
当n=1时,T1=S1,
当n≥2时,
故所求的正整数n存在,其最小值是2.
知识点
19.解不等式:
正确答案
原不等式变形为
所以,原不等式可化为
即:
即:
故原不等式解集为{x|2<x<3}
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析