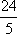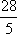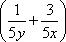- 函数的值域及其求法
- 共87题
1
题型：
单选题
|
椭圆
A
B
C
D
正确答案
B
解析
因为A，B为左，右顶点，F1，F2为左，右焦点，
所以|AF1|＝a－c，|F1F2|＝2c，|F1B|＝a＋c.
又因为|AF1|，|F1F2|，|F1B|成等比数列，
所以(a－c)(a＋c)＝4c2，即a2＝5c2.
所以离心率
知识点
函数的值域及其求法
1
题型：填空题
|
已知函数
正确答案
9。
解析
由值域为
∴
∴
∵不等式
知识点
函数的值域及其求法一元二次不等式的解法
1
题型：
单选题
|
若正数x，y满足x＋3y＝5xy，则3x＋4y的最小值是( )
A
B
C5
D6
正确答案
C
解析
∵x＋3y＝5xy，∴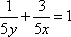
∴3x＋4y＝(3x＋4y)×1＝(3x＋4y)
＝
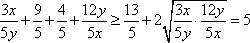
当且仅当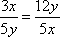
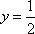
知识点
函数的值域及其求法
1
题型：填空题
|
若正实数X，Y 满足2X+Y+6=XY ， 则XY 的最小值是 。
正确答案
18
解析
运用基本不等式，
知识点
函数的值域及其求法
1
题型：
单选题
|
为了普及环保知识，增强环保意识，某大学随即抽取30名学生参加环保知识测试，得分（十分制）如图所示，假设得分值的中位数为
A
B
C
D
正确答案
D
解析
计算可以得知，中位数为5.5，众数为5所以选D
知识点
函数的值域及其求法
下一知识点 : 函数的图象与图象变化
扫码查看完整答案与解析