函数的值域及其求法
共87题

· 函数的值域及其求法

函数的值域及其求法
共87题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 16 分

18．已知函数，常数。

（1）设，证明：函数在上单调递增；

（2）设且的定义域和值域都是，求常数的取值范围。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的定义域及其求法函数的值域及其求法利用导数研究函数的单调性利用导数求函数的最值利用导数求参数的取值范围

题型：简答题

简答题 · 16 分

18.某水库堤坝因年久失修，发生了渗水现象，当发现时已有200m2的坝面渗水。经测算知渗水现象正在以每天4m2的速度扩散，当地政府积极组织工人进行抢修。已知每个工人平均每天可抢修渗水面积2m2,每人每天所消耗的维修材料费75元，劳务费50元，给每人发放50元的服装补贴，每渗水1m2的损失为250元。现在共派去x名工人,抢修完成共用n天。

（Ⅰ）写出n关于x的函数关系式；

（Ⅱ）要使总损失最小，应派去多少名工人去抢修(总损失＝渗水损失＋政府支出)。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的值域及其求法

题型：单选题

单选题 · 5 分

2.已知三角函数y=sin x是奇函数，则y=2sin(2x+)是三角函数，所以y=2sin(2x+)是奇函数。以上推理错误的是（）

A大前提

B小前提

C推理形式

D以上都正确

正确答案

解析

∵y=2sin(2x+)是三角函数型的复合函数，奇偶性与y=sin x不同，为非奇非偶函数,∴“y=2sin(2x+)是三角函数”这个小前提是错误的，从而导致结论错误，故选B。

知识点

函数的值域及其求法

题型：单选题

单选题 · 5 分

12.抛物线x2=8y的焦点为F，点P(x，y)为该抛物线上的动点，若点A(0，-2)，则的最大值是（）

正确答案

解析

由题意知y≥0，则焦点F(0，2)，|PF|=y+2

|PA|= =

当y=0时，=1；

当y>0时，1< = = ≤(当且仅当y=2时取等号).

所以1≤≤，所以的最大值是.

知识点

函数的值域及其求法

题型：单选题

单选题 · 5 分

6．已知函数f(x)= 则下列结论正确的是（）

Af(x)是偶函数

Bf(x)是增函数

Cf(x)是周期函数

Df(x)的值域为[-1，+∞)

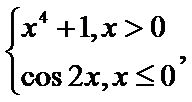
正确答案

解析

当x=1,f(1)=2,当x=-1,f(-1)=cos(-2)=cos2.所以A错。事实上，在不对称的区间上都是没有奇偶性的；

函数y=cos2x在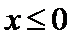时是没有奇偶性的，也不是单调递增或者递减，因此选项B是错的；

函数y=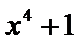在x>0时没有周期性；

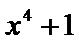
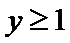
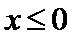
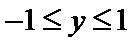
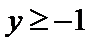
函数y=在x>0时，值域是，函数y=cos2x在时，值域是，所以，最终的结果是值域为[-1，+∞)。也可以根据图像可以很容易看出，整个函数的值域是的。

A选项不正确，B选项不正确，C选项不正确，所以选D选项。

考查方向

本题主要考查了分段函数的基本性质，三角函数的单调性、奇偶性，值域等。

解题思路

1.对每一个选项进行判断即可；

2.也可以画出图像，直接判断。

A选项不正确， B选项不正确， C选项不正确，D选项正确。

易错点

1、本题不容易想到在x>0时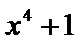的值域，在这里是部分图像；

2、对于cos2x在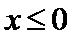时是没有奇偶性的，也不是单调递增或者递减；

3、整个函数在定义域中的值域是求它们的交集容易出错。

知识点

函数的值域及其求法函数单调性的判断与证明函数奇偶性的判断函数的周期性

继续学习学习下一知识点

下一知识点 : 函数的图象与图象变化

百度题库 > 高考 > 文科数学 > 函数的值域及其求法

扫码查看完整答案与解析