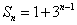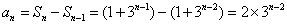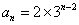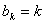- 数列
- 共2612题
已知函数


(1)求函数
(2)若关于


(3)数列


求
正确答案
见解析。
解析
(1)由f(x)=a x2+bx+1,所以f′(x)=2ax+b,
因为函数f(x)=a x2+bx+1在x=3处的切线方程为y=5x﹣8,所以切点为(3,7)。
则
所以f(x)=x2﹣x+1;
(2)由(1)知f(x)=x2﹣x+1,
关于x的方程f(x)=kex恰有两个不同的实根,
即x2﹣x+1=k•ex有两个不同的实根,也就是k=e﹣x(x2﹣x+1)有两个不同的实根。
令g(x)=e﹣x(x2﹣x+1),
则g′(x)=(2x﹣1)e﹣x﹣(x2﹣x+1)e﹣x
=﹣(x2﹣3x+2)e﹣x=﹣(x﹣1)(x﹣2)e﹣x
由g′(x)=0,得x1=1,x2=2。
所以当x∈(﹣∞,1)时,g′(x)<0,g(x)在(﹣∞,1)上为减函数;
当x∈(1,2)时,g′(x)>0,g(x)在(1,2)上为增函数;
当x∈(2,+∞)时,g′(x)<0,g(x)在(2,+∞)上为减函数;
所以,当x=1时,g(x)取得极小值g(1)=

函数y=k与y=g(x)的图象的大致形状如下,
由图象可知,当k=

(3)由2a1=f(2)=22﹣2+1=3,所以


又
所以an+1>an>1。
又
则

所以
=
=


又S=
故
知识点
已知数列





则
正确答案
解析
略
知识点
已知数列




(1)求数列
(2)设数列



(3)在第(2)问的条件下,若对于任意的


正确答案
(1)
(2)
(3)
解析
(1)由题意可知,
当

当

所以
(2)由(1)可知

当

当


当

当


……
当



以上

又


同理,当

所以,当

因此,当



当



故数列


(3)由(2)可知
①当

所以




②当

所以


综上,
因此,若对于任意的


故实数

知识点
已知


正确答案
-1/2
解析
略
知识点
在2012年8月15日那天,某物价部门对本市的5家商场的某商品的一天销售量价格进行调查,5家商场的售价x元和销售量y件之间的一组数据如下表所示:
由散点图可知,销售量y与价格x之间有较强的线性相关关系,其线性回归直线方程是:
正确答案
10
解析






∵其线性回归直线方程是:
∴

即30+n=﹣3.2(40+m)+200,又m+n=20,
解得m=n=10
故答案为:10。
知识点
设函数









正确答案
解析
略
知识点
已知等差数列{an}的前n项和为Sn,a4+a8=2,S11= 。
正确答案
11
解析
由等差数列的性质可得a1+a11=a4+a8=2,
故S11=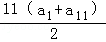
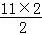
故答案为:11
知识点
一个三角形数表按如下方式构成(如图:其中项数




(1)求第2行和第3行的通项公式

(2)证明:数表中除最后2行外每一行的数都依次成等差数列,并求


(3)若







正确答案
见解析
解析
(1)

(2)由已知,第一行是等差数列,假设第

则由



由于



得
于是
即





(3)

令




令




知识点
已知函数

(1)求b1,b2的值;
(2)求数列{bn}的通项公式;
(3)求证:
正确答案
见解析。
解析
(1)∵f(x)=
∴a2=f(a1)=

由bn=


(2)∵an+1=

∴bn+1=



又b1=
∴lgbn+1=2lgbn,
又lgb1=lg
∴{lgbn}是以2为公比,首项为﹣lg2的等比数列。
故lgbn=(﹣lg2)×2n﹣1=lg
∴bn=
(3)由(2)得Tn=



当n≤3时,Tn≤




当n>3时,Tn=







又当n>3时,2n﹣1=(1+1)n﹣1>1+

∴Tn<



=
=




综上,Tn<
知识点
设数列









(1)求数列
(2)求证:对任意

(3)设





正确答案
见解析
解析
(1)因为



所以


即数列


所以
(2)解法一:
因为


猜测:

用数学归纳法证明:
①当

②假设当





由①,②得,当


解法二:
所以
而



(3)由(1)、(2)知

所以
所以
由

因为

当



当



所以,



由


所以,所求实数
知识点
已知数列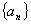
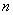
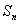
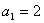
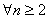
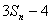
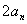
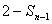
⑴求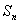
⑵对任意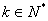
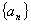
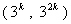
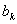
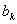
正确答案
见解析。
解析
解:⑴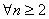
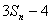
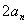
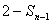
所以,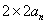
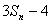
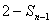
因为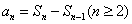
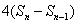
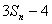
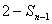
即
又因为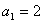
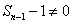
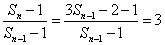
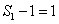
所以数列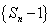
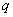
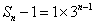
⑵由⑴得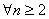
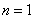
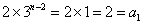
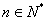
任意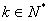
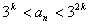
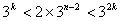
(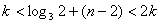
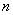
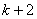
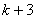
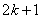
知识点
等差数列{an}中,a1,a2,a3分别是下表第一、二、三行中的某一个数,且a1,a2,a3中的任何两个数不在下表的同一列。
则a4的值为( )
正确答案
解析
由题意可得 a1 =3,a2 =8,a3=13,故此等差数列的公差为5,故a4=a3+d=18,
故选A。
知识点
已知数列{an}满足:a1=1,a2=a(a≠0),
(1)判断数列
(2)求an;
(3)当a=1时,令
正确答案
见解析。
解析
(1)由an+2=p•

令cn=
∵a≠0,
∴c1≠0,故
数列
(2)∵数列{cn}是首项为a,公比为p的等比数列,
∴cn=c1•pn﹣1=a•pn﹣1,
即
当n≥2时,an=



∵a1满足上式,
∴an=an﹣1
(3)∵


∴当a=1时,bn=
∴Sn=1×p1+2×p3+…+n×p2n﹣1,①
p2Sn=1×p3+…+(n﹣1)p2n﹣1+n×p2n+1②
∴当p2≠1,即p≠±1时,①﹣②得:(1﹣p2)Sn=p1+p3+…+p2n﹣1﹣np2n+1,
知识点
已知数列




正确答案


解析
略
知识点
数列{an}的前n项和为Sn,
(1)设bn=an+n,证明:数列{bn}是等比数列;
(2)求数列{nbn}的前n项和Tn;
(3)若cn=

正确答案
见解析。
解析
(1) 因为
当n=1时,2a1=﹣1,则a1=﹣
当n≥2时,
所以2an﹣an﹣1=﹣n﹣1,即2(an+n)=an﹣1+n﹣1,
所以

所以数{bn}是首项为

所以
(2) 由(1)得
所以 ①
②
②﹣①得:
(3)由(1)知
∴cn=n
而

=

所以
故不超过P的最大整数为2013.…
知识点
扫码查看完整答案与解析