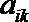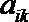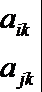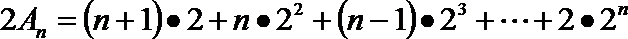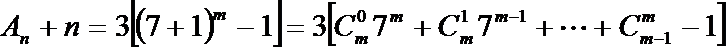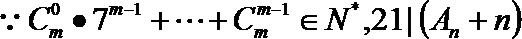- 数列
- 共2612题
18.如图所示的三角形数阵叫“莱布尼茨调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设a=


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.等比数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.对于各数互不相等的正数数组(








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.在数列




(1)若

(2)证明:当

(3)设集合

正确答案
(1)因为
由
所以
因为
所以
所以数列
(2)由已知
假设

则
可得

所以
所以数列
(3)设存在实数
所以
当
当
所以,当且仅当
当

综上,在区间[1,a]上存在实数b,使
解析
解析已在路上飞奔,马上就到!
知识点
6.在一条南北方向的步行街同侧有8块广告牌,牌的底色可选用红、蓝两种颜色,若只要求相邻两块牌的底色不都为红色,则不同的配色方案共有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.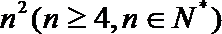
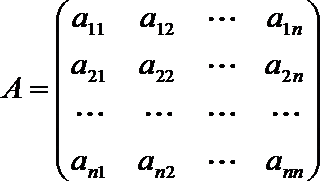
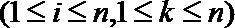
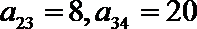
(1) 求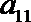
(2) 计算行数列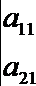
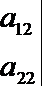
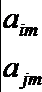
(3) 设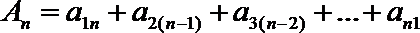
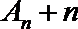
正确答案
解:(1)由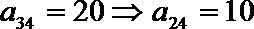
由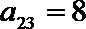
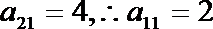
由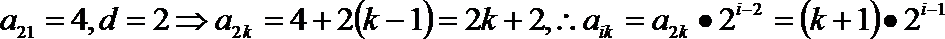
(2)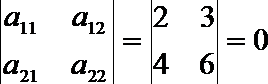
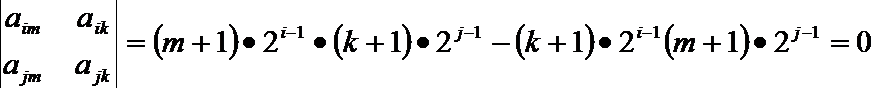
(3)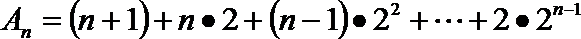
以上两式相减得: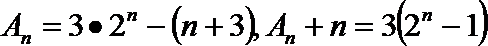
当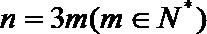
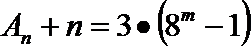
当m=1时,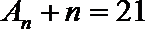
当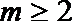
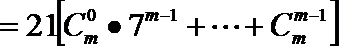
解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列



(1)求数列
(2)若函数

(3)设






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.有



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知



正确答案

解析
解析已在路上飞奔,马上就到!
知识点
19.设数列
上表共有



(1)求证:数列
(2)若

正确答案
(1)由题设易知,

设表中的第

显然


它们的平均数分别是

于是
故数列
(2)
解析
解析已在路上飞奔,马上就到!
知识点
14.数列


若







正确答案
2;

解析
解析已在路上飞奔,马上就到!
知识点
15.在各项都为正数的等比数列

(Ⅰ)求数列
(Ⅱ)若数列



正确答案
(Ⅰ)设各项都为正数的等比数列



由①②消去



所以数列
(Ⅱ)






故n=8或9时,
解析
解析已在路上飞奔,马上就到!
知识点
20.正整数数列

(Ⅰ)写出数列
(Ⅱ)将数列




(Ⅲ)求最小的正整数

正确答案
(Ⅰ)




(Ⅱ)由(Ⅰ)可知


猜想使


对






归纳易得:

故当

因此
(Ⅲ)由(Ⅱ)可知,

则


由(*)式可知,当

因此,当

而当



进而考虑
由


故使得

解析
解析已在路上飞奔,马上就到!
知识点
5.数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析