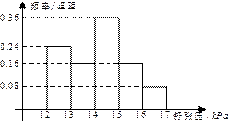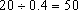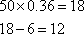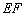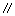- 诱导公式的作用
- 共73题
数列{an}的通项公式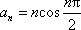
正确答案
解析
∵函数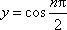
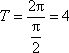
∴可分四组求和:
a1+a5+…+a2 009=0,
a2+a6+…+a2 010=-2-6-…-2 010=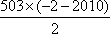
a3+a7+…+a2 011=0,
a4+a8+…+a2 012=4+8+…+2 012=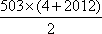
故S2 012=0-503×1 006+0+503×1 008=503×(-1 006+1 008)=1 006
知识点
三角形ABC中,





正确答案
见解析。
解析
由
由已知得
从而

由正弦定理得

所以
知识点
设函数f(x)=sinxcosx-cos(x+π)cosx(x∈R)。
(1)求f(x)的最小正周期;
(2)若函数y=f(x)的图象按b=平移后得到函数y=g(x)的图象,求y=g(x)在上的最大值。
正确答案
见解析。
解析
知识点
对于项数为m的有穷数列数集





(1)若各项均为正整数的数列

(2)设



(3)设m=100,常数



求
正确答案
见解析。
解析
(1)数列
(2)因为

所以
因为

所以

因此,
(3)对




比较大小,可得
因为




又
从而



因此
=
=
=


知识点
为了研究某药品的疗效,选取若干名志愿者进行临床实验。所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13), [13,14),[14,15),[15,16]。将其按从左到右的顺序分别编号为第一组,第二组,……,第五组。右图是根据试验数据制成的频率分布直方图。已知第一组和第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为
正确答案
解析
第一组与第二组频率之和为0.24+0.16=0.4
知识点
数列{an}满足a1=1,nan+1=(n+1)an+n(n+1),n∈N*。
(1)证明:数列{
(2)设bn=3n•
正确答案
见解析。
解析
(1)∵nan+1=(n+1)an+n(n+1),
∴
∴
∴数列{
(2)由(1)知,
∴
bn=3n•
∴

①﹣②得
=
=
∴
知识点
如图2,四边形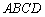
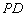
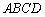
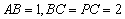
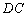
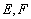
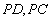
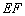
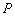
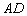
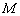
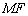
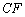
(1)证明: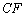
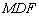
(2)求三棱锥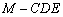
正确答案
见解析。
解析
知识点
正五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个正五棱柱对角线的条数共有
正确答案
解析
正五棱柱中,上底面中的每一个顶点均可与下底面中的两个顶点构成对角线,所以一个正五棱柱对角线的条数共有
知识点
若tanα>0,则( )
正确答案
解析
∵tanα>0,∴
知识点
在ABC中,角A、B、C的对边分别为a、b、c,且角A、B都是锐角,a=6,b=5 ,
(1) 求

(2) 设函数

正确答案
见解析。
解析
(1)由正弦定理

∵A、B是锐角,∴

由
(2)由(1)知
∴
知识点
扫码查看完整答案与解析