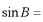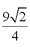- 诱导公式的作用
- 共73题
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4。
(1)从袋中随机抽取一个球,将其编号记为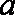
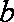
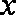
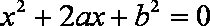
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,若以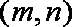
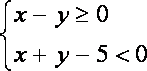
正确答案
见解析。
解析
(1)基本事件(a,b)有:(1,2) (1,3) (1,4) (2,1) (2,3) (2,4) (3,1) (3,2) (3,4) (4,1) (4,2) (4,3)共12种。
∵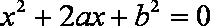
记“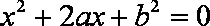
∴PA.=
(2)基本事件(m,n)有:(1,1) (1,2) (1,3) (1,4) (2,1) (2,2) (2,3) (2,4) (3,1) (3,2) (3,3) (3,4) (4,1) (4,2) (4,3) (4,4)共16种。
记“点P落在区域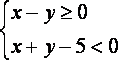
(1,1) (2,1) (2,2) (3,1) 共4种。∴PB.=
知识点

正确答案
解析
原式
知识点
在△ABC中,角A,B,C的对边分别为a,b,c,已知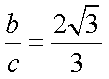
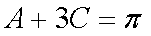
(1)求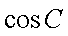
(2)求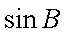
(3)若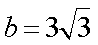
正确答案
(1)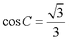
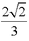
解析
解析:
(1)因为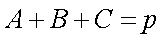
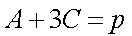
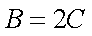
又由正弦定理,
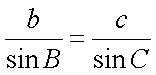
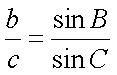
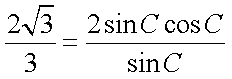
化简得,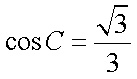


(2)因为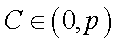
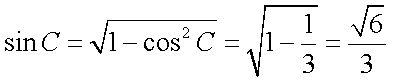
所以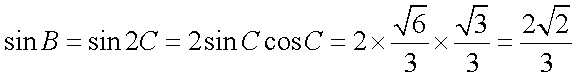
(3)因为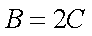
所以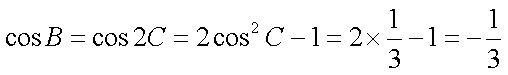
所以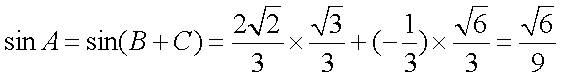
因为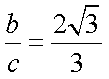
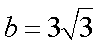
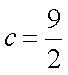
所以△ABC的面积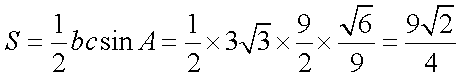
知识点
已知函数
(1) 当


(2) 讨论函数
(3)若函数



正确答案
见解析。
解析
(1)当
则

函数


(2)
当



则函数

当


由

由

故函数


在区间
(3)因为函数



令








知识点
已知


(1)求
(2)当

正确答案
见解析
解析
(1)解不等式:






(2)需证明:
只需证明
即需证明
证明:

知识点
设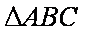
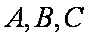
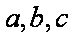
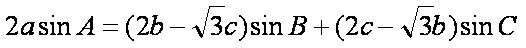
(1)求角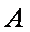
(2)若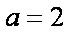
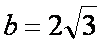
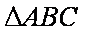
正确答案
见解析
解析
(1)由已知及正弦定理可得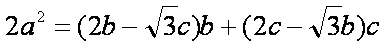
整理得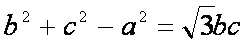
所以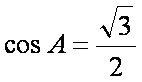
又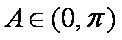
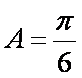
(2)由正弦定理可知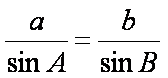
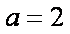
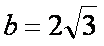
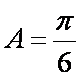
所以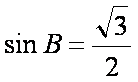
又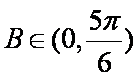
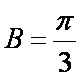
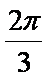
若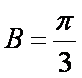
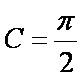
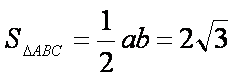
若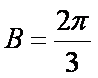
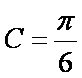
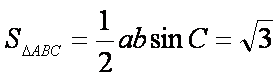
知识点
在△ABC中,角A,B,C的对边分别为a,b,c,且
(1)求cosB的值;
(2)若


正确答案
见解析。
解析
(1)由正弦定理得
因此
(2)由
所以
知识点
将边长为2的正△ABC沿BC边上的高AD折成直二面角B﹣AD﹣C,则三棱锥B﹣ACD的外接球的表面积为 _________ 。
正确答案
5π
解析
根据题意可知三棱锥B﹣ACD的三条侧棱BD、DC、DA两两互相垂直,所以它的外接球就是它扩展为长方体的外接球,
∵长方体的对角线的长为:

∴球的直径是

∴三棱锥B﹣ACD的外接球的表面积为:4π×
故答案为:5π
知识点
已知函数
(1)当

(2)当


正确答案
见解析
解析
(1)解:原不等式可化为
当


当


当



综上所述:原不等式的解集为
(2)原不等式可化为
∵

即
故

当




∴实数

知识点
已知全集


正确答案
解析




故选:B
知识点
扫码查看完整答案与解析