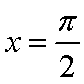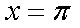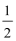- 诱导公式的作用
- 共73题
在







(1)求角
(2)若


正确答案
(1)
解析
(1)在


∴


∴

又因为

(2)在


即


而

知识点
下列命题中真命题的编号是 ,(填上所有正确的编号)
①向量与向量共线,则存在实数λ使=λ(λ∈R);
②,为单位向量,其夹角为θ,若|﹣|>1,则
③A、B、C、D是空间不共面的四点,若





④向量







⑤若向量
正确答案
②③
解析
①由向量共线定理可知,当
②若|﹣|>1,则平方得



③


④若足









⑤当

知识点
在锐角△ABC 中,角 A,B,C 所对边分别为 a,b,c,且 bsinAcosB=(2c-b)sinBcosA。
(1)求角A;
(2)已知向量


正确答案
见解析。
解析
(1)在锐角△ABC 中,由 bsinAcosB=(2c﹣b)sinBcosA利用正弦定理可得
sinBsinAcosB=2sinCsinBcosA﹣sinBsinBcosA,
故有sinBsin(A+B)=2sinCsinBcosA,解得

(2)由题意可得


由于 




∴

故

知识点
函数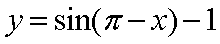
正确答案
解析
略
知识点
已知A(-l, 2),B(3,4),C(-2,1),D(-3,5),则向量

正确答案
解析



知识点

正确答案
解析
略
知识点
10.已知变量



正确答案
解析
由题意作出其平面区域,
则x+2y≥﹣5恒成立可化为图象中的阴影部分在直线x+2y=﹣5的上方,
则实数a的取值范围为[﹣1,1].
故答案为:[﹣1,1].
知识点
5.若圆的方程
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.若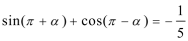
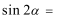
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析