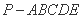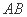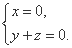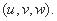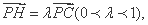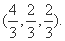- 用向量证明垂直
- 共1题
1
题型:简答题
|
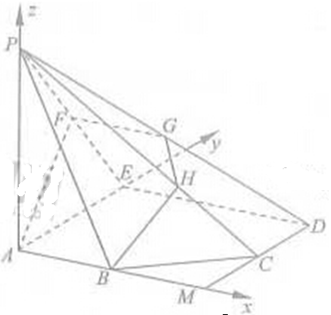
如图,正方形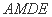
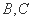
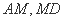
中,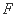
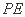
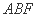
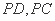

(1)求证: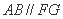
(2)若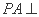
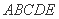
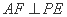
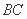
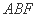
求线段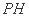
正确答案
见解析。
解析
(1)在正方形中,因为B是AM的中点,所以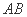
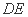
又因为
所以
因为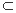
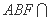
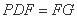
所以
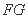
(2)因为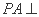
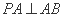
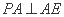
如图建立空间直角坐标系
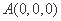
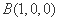
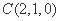

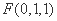
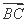
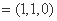
设平面ABF的法向量为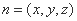
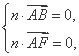
令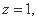
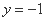
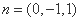
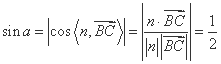
因此直线BC与平面ABF所成角的大小为
设点H的坐标为
因为点H在棱PC上,所以可设
即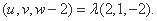
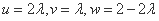
因为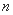
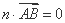
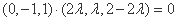
解得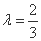
所以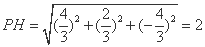
知识点
用向量证明垂直
下一知识点 : 用空间向量求直线间的夹角、距离
扫码查看完整答案与解析