函数奇偶性的判断_章节学习

1

题型：填空题

|

填空题 · 5 分

13．若函数f（x）=为偶函数，则a=

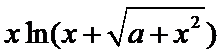
正确答案

1

解析

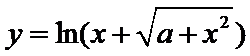
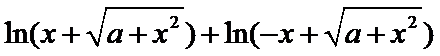
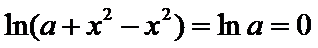
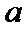
由题知是奇函数，所以 =，解得=1.

考查方向

本题考查了函数的奇偶性，是函数的性质的一部分内容，是基础题。

解题思路

本题考查了应用函数奇偶性，

易错点

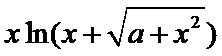
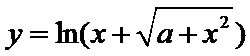
本题易在应用函数奇偶性的过程中易错。函数f（x）=为偶函数知是奇函数。用奇函数的定义可以得出结果.

知识点

函数奇偶性的判断

1

题型：单选题

|

单选题 · 5 分

3．下列函数中，既不是奇函数，也不是偶函数的是

A

B

C

D

正确答案

A

解析

令，则，即，，所以既不是奇函数也不是偶函数，而BCD依次是奇函数、偶函数、偶函数，故选．

考查方向

本题考查函数的奇偶性，属于基础题。

解题思路

逆带验证排除法。代入特殊值，对选项进行检验即可选出答案。

易错点

定义域关于原点对称是函数具有奇偶性的前提，奇函数、偶函数的表达式满足的关系不要弄错。

知识点

函数的单调性及单调区间函数奇偶性的判断

1

题型：简答题

|

简答题 · 12 分

设函数的定义域均为，且是奇函数，是偶函数，，其中为自然对数的底数．

26.求的解析式，并证明：当时，；

27.设，证明：当时，．

第(1)小题正确答案及相关解析

正确答案

，证明见解析

解析

试题分析：本题属于导数应用中的基本问题，题目的难度是逐渐由易到难，由函数的奇偶性形成方程组求解出的解析式并用均值不等式去证明函数不等式；由的奇偶性及 ① 得 ②．

联立①②解得．当时，，故． ③又由基本不等式，有，即． ④

考查方向

本题考查了利用方程思想求解析式和证明函数不等式的方法；导数常应用在求函数的单调区间，极值、最值及恒成立问题等级的处理，最常用的方法是最值法和“分离参数法”。

解题思路

本题考查导数的应用，解题步骤如下：函数的奇偶性形成方程组求解出的解析式并用均值不等式去证明函数不等式。

易错点

对求解析式方法不熟导致出错。

第(2)小题正确答案及相关解析

正确答案

详见解析；

解析

试题分析：本题属于导数应用中的基本问题，题目的难度是逐渐由易到难，由函数的奇偶性形成方程组求解出的解析式并用均值不等式去证明函数不等式；由的奇偶性及 ① 得 ②．

联立①②解得．当时，，故． ③又由基本不等式，有，即． ④

考查方向

本题考查了利用方程思想求解析式和证明函数不等式的方法；导数常应用在求函数的单调区间，极值、最值及恒成立问题等级的处理，最常用的方法是最值法和“分离参数法”。

解题思路

本题考查导数的应用，解题步骤如下：

观察所证不等式的结构构建新函数去证明所求不等式。

易错点

未发现的关系和用到第（1）问的结论。

1

题型：简答题

|

简答题 · 5 分

10．若偶函数的定义域为，则=

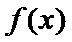
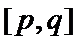
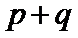
正确答案

0

解析

p+q=0

考查方向

考查偶函数的定义域的特点

解题思路

偶函数定义的特点是关于原点对称

易错点

没有掌握偶函数的定义的特点

知识点

函数奇偶性的判断

1

题型：单选题

|

单选题 · 5 分

4．下列函数中，既是偶函数，又在上是单调减函数的是（）

A

B

C

D

正确答案

B

解析

由函数的奇偶性及单调性的性质可知，B和D选项为偶函数，又知，D选项在上不是单调函数，所以此题选B.

考查方向

函数的单调性；函数的奇偶性

解题思路

根据函数单调性及奇偶性的性质，逐个选项判断

易错点

函数单调性判断错误，函数奇偶性判断错误

知识点

函数单调性的判断与证明函数奇偶性的判断

1

题型：填空题

|

填空题 · 5 分

13．设是定义在上的偶函数，对任意的，都有，且当时，，若关于的方程在区间内恰有三个不同实根，则实数的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数奇偶性的判断

1

题型：单选题

|

单选题 · 5 分

18．下列函数中，既是偶函数，又在上递增的函数的个数是（）

①

②

③

④

A1个

B2个

C3个

D4个

正确答案

A

解析

由图可知，符合要求的函数只有一个，所以选A．

考查方向

本题主要考查简单三角函数的图像与性质以及函数图像的变换，属于中档题．

解题思路

根据图像变换，先画出、、、四个函数的图像，然后根据题设条件之间判断即可．

易错点

与图像的变换极易混淆．

知识点

函数单调性的判断与证明函数奇偶性的判断

1

题型：单选题

|

单选题 · 5 分

2．下列函数中，值域为的偶函数是（）

A

B

C

D

正确答案

C

解析

因为的值域为，所以排除选项A；因为，即是奇函数，所以排除选项B；因为的值域为，所以排除选项D；因为的值域为，且，即为偶函数，所以选C选项。

考查方向

本题主要考查了函数的值域和函数的奇偶性。

解题思路

通过逐一验证函数的值域和奇偶性进行排除得到答案。

易错点

本题易在判定选项D的值域时出现错误，易忽视，而不是。

知识点

函数的值域函数奇偶性的判断

1

题型：单选题

|

单选题 · 5 分

18．下列函数中，既是偶函数，又在上递增的函数的个数是（）

①

②

③

④

A1个

B2个

C3个

D4个

正确答案

A

解析

① 的定义域，在上不连续，且时，；时，，所以在上没有单调性，不合题意。

② ，在上单调递减，不合题意。

③ ，是偶函数且在上单调递增，满足题意。

④不是偶函数，不满足题意。所以满足题设条件的只有③一个函数。

考查方向

本题主要考查了函数的奇偶性以及三角函数的单调性，

解题思路

本题考查函数的奇偶性以及三角函数的单调性，可以先化简函数的解析式，再作出判断。

易错点

本题必须注意正切和余切函数的定义域以及分段函数单调性的要求，忽视则会出现错误。

知识点

函数单调性的判断与证明函数奇偶性的判断

1

题型：单选题

|

单选题 · 5 分

2. 下列函数中，值域为的偶函数是（）

A

B

C

D

正确答案

C

解析

由（A）的值域为 B 值域为Ｒ（D）函数的值域都不是从而排除Ａ、Ｂ、Ｄ，选择Ｃ答案。

考查方向

本题主要考查了函数值域的求法及偶函数的概念和判断方法

解题思路

先由函数的值域为而排除不符合题意的选项，再判断其奇偶性从而确定正确答案。

易错点

不会求值域或不会判断偶函数而出错

知识点

函数的值域函数奇偶性的判断

热门试卷

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点