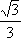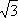集合的概念及运算
共1168题

集合的概念及运算
共1168题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

函数图像上存在不同的三点到原点的距离构成等比数列，则以下不可能成为公比的数是--------------- （）

正确答案

解析

略

知识点

集合的含义

题型：单选题

单选题 · 5 分

已知集合，，且，那么的值可以是（）

A-1

正确答案

解析

略

知识点

集合的含义

题型：简答题

简答题 · 18 分

若对任意的，存在正常数，恒有成立，则叫做Γ数列，

（1）若公差为的等差数列是Γ数列，求的值；

（2）记数列的前n项和为，证明：若是Γ数列，则也是Γ数列；

（3）若首项为1，公比为的等比数列是Γ数列，当时，求实数的取值范围。

正确答案

见解析

解析

（1）由题意 ………2分

由n的任意性，得d=0………………………………………………………………4分

（2）由是Γ数列得，存在正常数，

恒有成立，

即……………………………………………………6分

所以

…………………………………………………………………………9分

因为是正常数，所以是Γ数列，………………………10分

（3）由（1）知当时是Γ数列………………………………11分

显然当时不是Γ数列。

……………………………………………………………13分

若对任意的，成立，则必有，

所以，…………………………………………15分

当时，上式恒成立；

当时，上式化为，解得，………………17分

所以，的取值范围是

知识点

集合的含义

题型：单选题

单选题 · 5 分

已知，则

正确答案

解析

略

知识点

集合的含义

题型：单选题

单选题 · 5 分

设集合A={x|x2﹣2x﹣3＜0，x∈R}，集合B=（﹣2，2），则A∩B为（　　）

A（﹣1，2）

B（﹣2，﹣1）

C（﹣2，3）

D（﹣2，2）

正确答案

解析

A={x|x2﹣2x﹣3＜0，x∈R}=（﹣1，3）

∵B={﹣2，2}，

∴A∩B=（﹣1，2）

故选：A。

知识点

集合的含义

题型：单选题

单选题 · 5 分

在实数集R中定义一种运算“⊕”，具有性质：

①对任意a，b∈R，a⊕b=b⊕a；

②对任意a∈R，a⊕0=a；

③对任意a，b，c∈R，（a⊕b）⊕c=c⊕（ab）+（a⊕c）+（b⊕c）﹣2c。

函数f（x）=x⊕（x＞0）的最小值为（　　）

正确答案

解析

根据题意，得

f（x）=x⊕=（x⊕）⊕0=0⊕（x•）+（x⊕0）+（⊕0 ）﹣2×0=1+x+

即f（x）=1+x+

∵x＞0，可得x+≥2，当且仅当x==1，即x=1时等号成立

∴1+x+≥2+1=3，可得函数f（x）=x⊕（x＞0）的最小值为f（1）=3

故选：B

知识点

集合的含义

题型：简答题

简答题 · 13 分

已知函数.

（1）求的单调区间；

（2）是否存在实数，使得函数的极大值等于？若存在，求出的值；若不存在，请说明理由.

正确答案

见解析

解析

（1）的定义域为.

，

即 . ……………………2分

令，解得：或.

当时，，故的单调递增区间是.……………………3分

当时，

，随的变化情况如下：

所以，函数的单调递增区间是和，单调递减区间是.………………5分

当时，

，随的变化情况如下：

所以，函数的单调递增区间是和，单调递减区间是.……………………7分

（2）当时，的极大值等于. 理由如下：

当时，无极大值.

当时，的极大值为，…………………8分

令，即解得或（舍）.……………………9分

当时，的极大值为. ……………………10分

因为，，

所以 .

因为，

所以的极大值不可能等于.……………………12分

综上所述，当时，的极大值等于.……………………13分

知识点

集合的含义

题型：单选题

单选题 · 5 分

已知集合，集合，则（）

A{1，2，3，4}

B{1，2，3，4，5，6}

C{2，3，4，5，6}

D{3，4}

正确答案

解析

略

知识点

集合的含义

题型：填空题

填空题 · 4 分

已知集合，集合，则_______。

正确答案

解析

略

知识点

集合的含义

题型：单选题

单选题 · 5 分

已知集合集合B={0，b，1﹣a}，且A∩B={1}，则A∪B=（　　）

A{0，1，3}

B{1，2，4}

C{0，1，2，3}

D{0，1，2，3，4}

正确答案

解析

∵A={3，a2}，集合B={0，b，1﹣a}，且A∩B={1}，

∴a2=1，解得：a=1或a=-1，

当a=1时，1﹣a=1﹣1=0，不合题意，舍去；

当a=-1时，1-a=1-（-1）=2，此时b=1，

∴A={3，1}，集合B={0，1，2}，

则A∪B={0，1，2，3}。

故选C

知识点

集合的含义

继续学习学习下一知识点

下一知识点 : 命题及其关系、充分条件与必要条件

百度题库 > 高考 > 理科数学 > 集合的概念及运算

扫码查看完整答案与解析