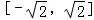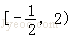- 简单的线性规划
- 共504题
设函数f(x)的定义域为D,若存在非零实数l使得对于任意x∈M(M⊆D),有x+l∈D,且f(x+l)≥f(x),则称f(x)为M上的l高调函数,如果定义域为R的函数f(x)是奇函数,当x≥0时,f(x)=|x﹣a2|﹣a2,且f(x)为R上的8高调函数,那么实数a的取值范围是
正确答案
解析
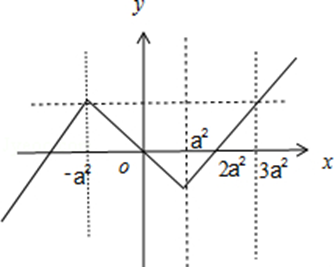
当x≥a2时f(x)=x﹣2a2,当0≤x<a2时f(x)=﹣x,再根据奇函数图象关于原点对称可作出f(x)的图象,如图所示。
由f(x)为R上的8高调函数,知f(x+8)≥f(x)恒成立,
由图象得8≥3a2﹣(﹣a2),即a2≤2,解得﹣

知识点
已知函数
(1)求
(2)若对于任意的


正确答案
(1)
(2)
解析
(1)解:
(2)解:

因为 

所以当 



所以 


故当 



知识点
已知函数

(1)若全集

(2)对任意


(3)设







正确答案
(1)

解析
(1)由已知得,

当且仅当


所以,
(2)由题得 
函数



(3)设


即
由


所以

知识点
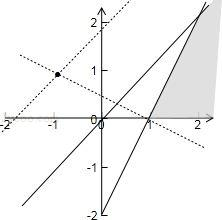
若实数x、y满足不等式组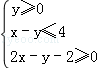
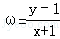
正确答案
解析
约束条件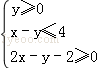

由图可知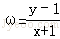
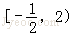
故答案为: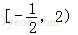
知识点
设
(1)当

(2)若对任意x∈R,

正确答案
见解析
解析
解析:
(1)f(x)=|x-a|≤3,即a-3≤x≤a+3.依题意,
由此得a的取值范围是[0,2],
(2)f(x-a)+f(x+a)=|x-2a|+|x|≥|(x-2a)-x|=2|a|,
当且仅当(x-2a)x≤0时取等号, 解不等式2|a|≥1-2a,得a≥。
故a的最小值为。
知识点
函数
(1)画出函数
(2)若不等式

正确答案
见解析
解析
(1)
(2) 由
又因为
解不等式

知识点
已知定义域为



(1)求
(2)若对任意的


正确答案
见解析
解析
(1)


当

又


综上所述
(2)




由

又

即



知识点
设函数
(1)求不等式
(2)

正确答案
见解析
解析
解析:
(1)
当
当
当
综上所述 
(2)易得


则只需

知识点
已知函数
(1)当
(2)如果


正确答案
(1)定义域:(-1,3),值域:(-∞,2](2)
解析
(1) 当
令
所以函数

令
所以
因此函数

(2) 解法一:



令
当


当


当





当


当


综上,

解法二:



由


令
所以

因此

知识点
巳知函数f(x)=|x-2|+2|x-a|(a∈R)。
(1)当a=1时,解不等式f(x)>3;
(2)不等式
正确答案
见解析
解析
解析:(1)



不等式的解集为
(2)




则


知识点
扫码查看完整答案与解析